Impulso – O que é? Teorema do impulso e Quantidade de movimento
O impulso da força resultante que atua sobre um corpo durante determinado intervalo de tempo é igual à variação da quantidade de movimento nesse intervalo.
Empurrar um corpo não é apenas exercer uma força sobre ele, mas exerce-la durante um tempo. Se a mesma força atua sobre um corpo durante intervalos de tempo diferentes, temos duas situações físicas distintas. Para entender o que faz essas duas situações serem diferentes precisamos compreender sobre uma nova grandeza: o impulso da força, representado por: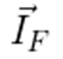 Para isso, precisamos analisar a relação entre a força e o intervalo de tempo. No cotidiano, uma pessoa deve se esforçar mais para realizar uma tarefa quando ela possui pouco tempo para isso, e pode se esforçar menos quando possui mais tempo.
Para isso, precisamos analisar a relação entre a força e o intervalo de tempo. No cotidiano, uma pessoa deve se esforçar mais para realizar uma tarefa quando ela possui pouco tempo para isso, e pode se esforçar menos quando possui mais tempo.
Na física, existe um tipo de compensação entre força e intervalo de tempo, que é expresso pela seguinte relação: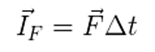 O impulso de uma força é uma grandeza vetorial, que possui sempre a mesma direção e o sentido da força.
O impulso de uma força é uma grandeza vetorial, que possui sempre a mesma direção e o sentido da força.
O impulso não possui uma unidade de medida própria, mas pode ser expresso por N.s (Newtons por segundo).
Utilizamos o impulso como uma grandeza auxiliar, com o intuito de emprega-la na obtenção de outras grandezas. Porém, para entender melhor como o impulso funciona, precisamos compreender o que é quantidade de movimento.
Quantidade de movimento
A quantidade de movimento de um corpo é representada por: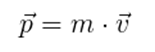 Podemos, então, dizer que:
Podemos, então, dizer que:
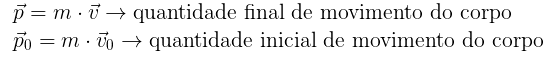
A quantidade de movimento também não tem unidade própria, sendo expressa por kg.m/s no SI.
Teorema do impulso
Imagine a seguinte situação: uma força resultante FR atua sobre um bloco de massa m, durante um intervalo de tempo Δt. Essa força exerce um impulso IF e, como consequência, a velocidade passa de v0 para v.
Sob a ação dessa força, o bloco adquire uma aceleração. Então temos: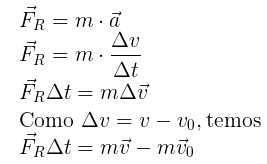
Sabemos que IF = F Δt, podemos dizer que: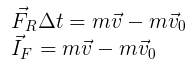
Vemos aqui que a diferença entre m.v e m.v0 é igual ao impulso. Portanto, o impulso varia de acordo com o produto de m.v, que é a quantidade de movimento de um corpo.
Anteriormente, vimos o que é a quantidade de movimento inicial e final. Portanto, podemos escrever o impulso da força como: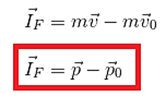 Como p – p0 é a variação da quantidade de movimento do corpo sob ação do impulso da força resultante, podemos escrever:
Como p – p0 é a variação da quantidade de movimento do corpo sob ação do impulso da força resultante, podemos escrever: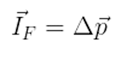 Esse é o Teorema do impulso.
Esse é o Teorema do impulso.
Imagine uma criança num balanço, com uma certa velocidade. Em um determinado instante, um amigo dessa criança aplica uma força sobre ela, dando-lhe um impulso. O resultado desse impulso é um aumento na quantidade de movimento que a criança possuía inicialmente.
Se pegarmos a quantidade de movimento que a criança tinha antes do empurrão e a quantidade de movimento após, veremos que a diferença entre as quantidades de movimento é exatamente o impulso dado pelo amigo, ou seja, ele ganhou uma certa quantidade de movimento, que é o impulso.
Conservação da quantidade de movimento
Considerando um sistema isolado de forças externas, temos que FR = 0. Usando essa informação na equação do impulso, temos: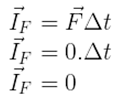 Além disso, pelo Teorema de Impulso, temos:
Além disso, pelo Teorema de Impulso, temos: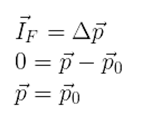 Podemos concluir que, em um sistema isolado, a quantidade de movimento permanece constante. Também, é possível reescrever esse princípio da seguinte maneira:
Podemos concluir que, em um sistema isolado, a quantidade de movimento permanece constante. Também, é possível reescrever esse princípio da seguinte maneira:
- Se a resultante das forças externas a um sistema for nula, a quantidade de movimento total desse sistema permanecerá constante.
Exercício resolvido
1) Uma mola está comprimida por dois blocos, A e B, de massa mA = 2 kg e mB = 3 kg, presos por um fio sobre o plano horizontal sem atrito. Quando o fio se rompe, o sistema é solto. Verifica-se que o bloco B adquire velocidade de 4 m/s. Assim, determine a velocidade adquirida pelo bloco A.
RESPOSTA:
Como a força do sistema bloco-mola é nula (sem atrito), podemos aplicar o Princípio da Conservação de Quantidade de Movimento.![]() Antes da mola ser solta, temos: p0 = 0. Depois que a mola é solta, o bloco A adquire vA e o bloco B vB. Em módulo, temos: p = mA(-vA) + mB(-vB).
Antes da mola ser solta, temos: p0 = 0. Depois que a mola é solta, o bloco A adquire vA e o bloco B vB. Em módulo, temos: p = mA(-vA) + mB(-vB).
Como todos os vetores estão na mesma direção (velocidade, quantidade de movimento, força…), podemos substituir as informações que temos acima:
0 = mA(-vA) + mB(-vB)
0 = 2vA + 3.4
2vA = 12
vA = 6 m/s









Deixe seu comentário