Força Centrípeta – O que é? Fórmulas, Exemplos e Exercícios Resolvidos
A força centrípeta é a força que puxa um objeto que está em movimento circular uniforme para o centro da trajetória. Ela tem o mesmo sentido da aceleração centrípeta e é perpendicular à velocidade vetorial do móvel.
O papel dessa força é desempenhado pelos mais variados tipos de forças, isolada ou somada com outras, como a tração em um fio, a força de atrito, o peso exercido pela Terra sobre um corpo e a reação normal de uma superfície.
De acordo com a Segunda Lei de Newton, se todo corpo em MCU tem aceleração, ele está sob a ação de uma força resultante. Embora aparentemente simples, essa conclusão é o fundamento básico do estudo da dinâmica do movimento circular.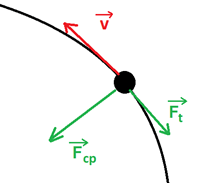
A força tem direção radial e aponta para o centro da curva. Nessa imagem, o corpo de massa m está em Movimento Circular Uniforme, sob aceleração centrípeta. Pela Segunda Lei de Newton (F = m.a), se esse corpo tem aceleração a, atua sobre ele a força resultante Fcp na mesma direção e no sentido da aceleração.
Essa força resultante que produz a aceleração centrípeta no corpo em MCU é a força centrípeta. Podemos, então, reescrever a Segunda Lei de Newton da seguinte forma: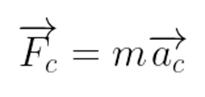
Sendo Fc a força centrípeta, m a massa do corpo e ac a aceleração centrípeta.
A aceleração centrípeta é dada por: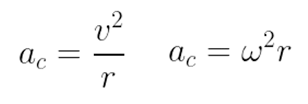
Sendo ac a aceleração centrípeta, v a velocidade vetorial do corpo, r o raio e ω a velocidade angular.
Lembrando que o módulo da aceleração centrípeta pode ser expresso nas duas fórmulas acima, temos, portanto, duas expressões para o módulo da força centrípeta.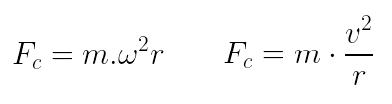
A força centrípeta é apenas a denominação particular da força resultante que atua sobre o corpo em MCU; não é um novo tipo de força. A aceleração centrípeta é constante, logo, a força centrípeta também é constante.
A força centrípeta, a velocidade vetorial e a aceleração angular se relacionam da seguinte forma: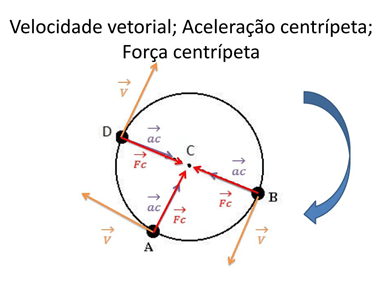
A força centrípeta atua na mesma direção da aceleração centrípeta, em direção ao centro da trajetória. Ambas são perpendiculares à velocidade.
Exercícios resolvidos
1) Um bloco de massa m = 2kg está sobre uma mesa horizontal sem atrito, preso ao ponto central O por um fio inextensível, girando com movimento circular uniforme. Sendo v = 4,0m/s o módulo da velocidade do boco e r = 5m o raio da circunferência descrita, determine:
A) a aceleração centrípeta;
B) a tração exercida pelo fio.
RESOLUÇÃO
A) ac = v²/r = 4²/ 0,5 = 32 m/s²
B) conhecendo a massa e a aceleração centrípeta do bloco, podemos aplicar a expressão Fc = m.ac em módulo: Fc = m.ac = 2,0 . 32 = 64N
Como a força centrípeta é a resultante das forças que atuam sobre o bloco, vamos determinar a tração T por meio dela. Para isso, precisamos representar as forças que atuam sobre o bloco:
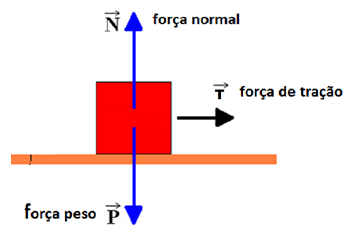
Como o plano é horizontal, a força peso e a força normal de equilibram, portanto a tração será igual à força centrípeta: T = Fc = 64 N
2) Um automóvel de massa 750kg faz uma curva circular plana e horizontal de raio 50m. Sabendo que o coeficiente de atrito estático entre os pneus e a pista é de μc = 0,8, determine:
A) a intensidade máxima e a força centrípeta que pode atuar sobre o automóvel enquanto ele faz a curva.
B) a máxima velocidade com que esse automóvel pode fazer a curva sem derrapar. Admita g = 10 m/s²
RESOLUÇÃO
A) como as forças verticais peso e normal se equilibram, a força resultante é a força de atrito estático. Sendo a força centrípeta a força resultante que atua sobre um corpo em MCU, temos que a força centrípeta é igual à força de atrito estático: Fc = fae
Como o módulo da força de atrito estático (seu valor máximo) é dado por μeN e, nesse caso, N = P, faremos: Fae = μeP = μe.m.g = 0,8 . 750 . 10 = 6 000 N
B) por meio da expressão da força centrípeta em função da velocidade, concluímos que, para a força centrípeta máxima, obtemos a velocidade máxima, pois os outros fatores (massa do móvel e raio da curva) não variam. Assim:
Fc = m . V²/r
6000 = 750 . V²/ 50
V= 20 m/s
Deixe seu comentário