Função Identidade – Definição, Exemplos e mais!

Considere uma função afim:

• f(x)=ax+b.

Se ‘a’ for 1 e ‘b’ for 0, então teremos f(x)=x, uma função identidade. Para dado valor de x, teremos o mesmo valor para f(x), que num gráfico seria o ‘y’. Portanto, se x=2, y=2. Se x=-5, y=-5 e assim por diante.

Dessa forma, o gráfico dessa função será uma reta diagonal que corta os quadrantes 1 e 3 e a origem (0,0) e por essa razão também é conhecida como bissetriz dos quadrantes ímpares.

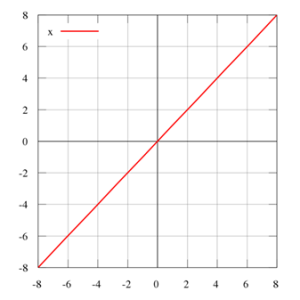
Repare que, para:

x=0, y=0

x=6, y=6

x=-4, y=-4

Essa função é dita bijetora pois cada elemento de X é associado a um único elemento de Y e vice-versa. Além disso é uma função ímpar pois f(-x) = -f(x).

Outros tipos de função

Repare que o gráfico seria muito parecido se a função fosse f(x)=x+b, onde b é um número qualquer. Porém, nesse caso, a reta estaria deslocada no eixo x em b, e não passaria pela origem.

Outra função parecida é a f(x)=-x. Repare que, por um sinal negativo, ela será a função identidade “espelhada”: para x=1, y=-1; para x= -4, y=4 e assim por diante, levando a uma reta diagonal, mas passando pelos segundo e quarto quadrantes.

É importante mencionar que, da mesma forma que um sinal negativo muda o comportamento da função, uma função do tipo f(x)=x² não fornece para f(x) o mesmo valor que x, e por isso não é uma função identidade.

Pode-se pensar num exemplo da física onde se queira colocar num gráfico a posição S em metros no eixo y e o tempo t em segundos no eixo x quando a velocidade é constante.

Assim, a função ficará S=t. Essa função é a função horária das posições para a velocidade constante S=S₀+v.t; porém, a posição inicial S₀ vale 0 e a velocidade v vale 1 m/s.

E então, para cada tempo, se terá uma posição de mesmo valor. Claro que aqui não teríamos um tempo negativo, mas, se houvesse, então o comportamento seria como de uma função identidade.

Aproveite e leia também:
Funções Trigonométricas – O que são? Função do Seno e Cosseno

Referências

Fonte: LANG, Serge. Basic mathematics. Frank Brothers, 1988.