Relações métricas do triângulo, do círculo e da circunferência
Em trigonometria, muitas vezes nos deparamos com problemas que nos pedem informações a respeito dos lados de um triângulo. Para descobrir essas informações usamos as relações métricas em triângulos. O mesmo pode ocorrer quando temos cordas, retas secantes ou retas tangentes em circunferências.
Relações métricas são expressões que relacionam a medida dos lados de um triângulo ou os seguimentos de uma circunferência. Veja, a seguir, quais são e como utilizá-las.
Relações métricas no triângulo retângulo
Vamos considerar um triângulo ABC, retângulo em A e o seguimento AD perpendicular ao lado BC, como mostra a figura abaixo: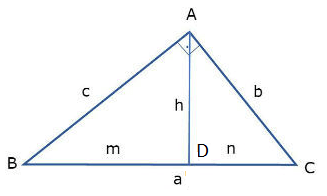 Primeiro, vamos definir cada um dos seguimentos desse triângulo:
Primeiro, vamos definir cada um dos seguimentos desse triângulo:
- BC = hipotenusa = a;
- AC = cateto = b;
- AB = cateto = c;
- BD = projeção do cateto c sobre a hipotenusa = m;
- CD = projeção do cateto b sobre a hipotenusa = n;
- AD = altura relativa a hipotenusa = h.
A altura h traçada nesse triângulo o separa em outros dois triângulos retângulos, que são semelhantes entre si e semelhantes ao triangulo ABC. Veja: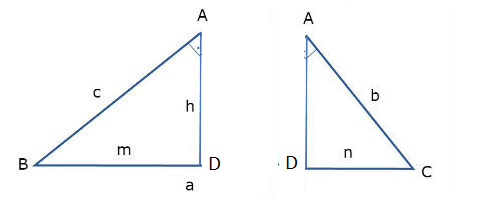 Sabemos que dois triângulos são semelhantes se possuírem dois ângulos correspondentes congruentes. Portanto, podemos dizer que os triângulos são semelhantes:
Sabemos que dois triângulos são semelhantes se possuírem dois ângulos correspondentes congruentes. Portanto, podemos dizer que os triângulos são semelhantes: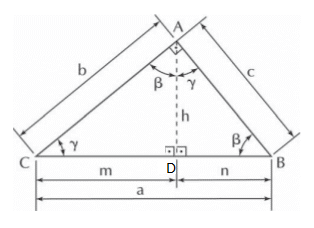
- ΔABC ~ ΔDBA ~ ΔDAC *Lembre-se: o sinal (~) quer dizer “semelhante”.
Observe os ângulos dos triângulos e veja a semelhança entre eles, por terem ângulos congruentes.
O sinal (Δ) quer nos informar que estamos tratando, nesse caso, de um triângulo.
Agora, usando essa semelhança, iremos mostrar quais são as relações trigonométricas.
- Da semelhança entre ΔABC e ΔDBA, podemos concluir que:
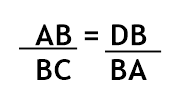 Como AB = c, DB = m, BC = a, BA = c, temos:
Como AB = c, DB = m, BC = a, BA = c, temos: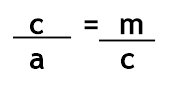 Disso, temos nossa primeira relação:
Disso, temos nossa primeira relação: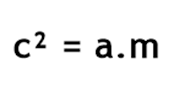
- Da semelhança entre ΔABC ~ ΔDAC, teremos:
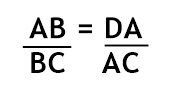
Como DA = h e AC = b, teremos: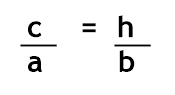 A segunda relação será:
A segunda relação será: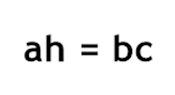 Continuando com esse método, teremos as outras relações:
Continuando com esse método, teremos as outras relações: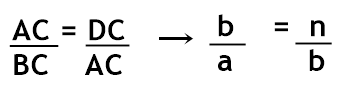 A terceira relação será:
A terceira relação será: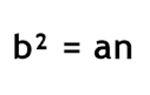
- Da semelhança ΔDBA ~ ΔDAC, temos:
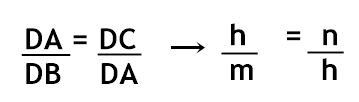
A quarta relação será: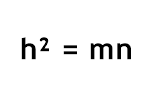
- Somando membro a membro, a primeira e terceira relação, teremos:

Portanto, a quinta relação será o próprio Teorema de Pitágoras.
- A primeira e quinta são chamadas de relações métricas no triângulo retângulo.
- A primeira e terceira podem ser generalizadas como: cateto² = hipotenusa, projeção, ou seja, são praticamente as mesmas.
Resumindo, teremos:
Relações métricas em um triângulo qualquer
Existem duas relações métricas que se aplicam a qualquer triângulo: lei dos cossenos e a lei dos senos. Veja, abaixo, as duas relações.
Lei dos senos
Em qualquer triângulo, as medidas dos lados são proporcionais aos senos dos ângulos opostos, ou seja: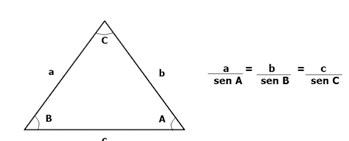
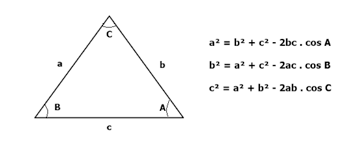
Lei dos cossenos
Em um triângulo, o quadrado da medida de um lado é igual à soma dos quadrados das medidas dos outros dois lados, menos duas vezes o produto das medidas desses lados pelo cosseno do ângulo que eles formam. Ou seja:
- a² = b² + c² – 2bc . cos A;
- b² = a² + c² – 2ac . cos B;
- c² = a² + b² – 2ab . cos C.
Relações métricas na circunferência
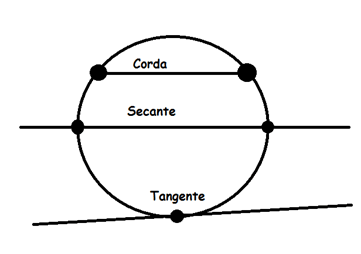
Vamos primeiramente definir três elementos da circunferência:
- Corda: seguimento que liga dois pontos na circunferência;
- Seguimento secante: uma das extremidades é um ponto fora da região circular;
- Seguimento tangente: seguimento que está sobre a circunferência.
A seguir, veremos as relações métricas na circunferência.
Cruzamento de duas cordas
Em toda circunferência, se duas cordas se cruzam, o produto das medidas de duas partes de uma é igual ao produto das medidas de duas partes de outra.
Ou seja, podemos dizer que: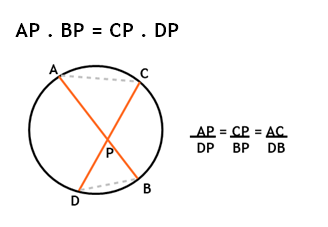
Dois seguimentos secantes a partir de um mesmo ponto
Em toda circunferência, se traçarmos dois seguimentos secantes a partir de um ponto, o produto da medida de um deles pela medida de sua parte externa é igual ao produto da medida do outro pela medida de sua parte externa.
Ou seja, podemos dizer que: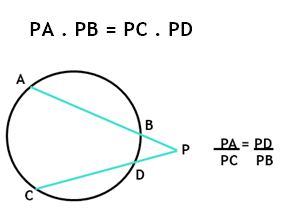
Seguimento secante e seguimento tangente a partir de um mesmo ponto
Em toda circunferência, quando traçamos a partir de um mesmo ponto um seguimento tangente e um seguimento secante, o quadrado da medida do seguimento tangente é igual ao produto da medida do seguimento secante pela medida de sua parte externa.
Ou seja, isso quer dizer que: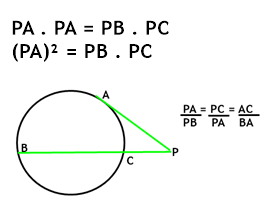
Exercícios resolvidos
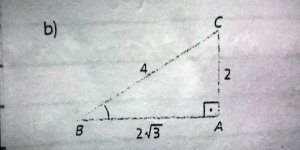
1) Calcule o valor de x na figura abaixo: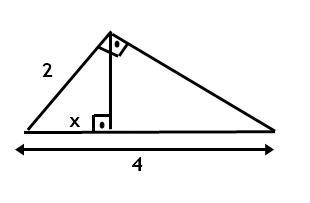 RESPOSTA:
RESPOSTA:
c² = am
2² = 4x
X= 1
2) Determine o valor de x na figura abaixo: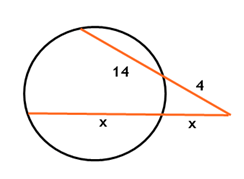 RESPOSTA:
RESPOSTA:
PA . PB = PC . PD
(14+4) . 4 = (x+x) . X
72 = 2x . X
2x² = 72
X² = 36
X = 6






Deixe seu comentário