Seno, Cosseno e Tangente -Tabela, Explicação e Como calcular (Passo a Passo)

Seno, Cosseno e Tangente são as medidas dos ângulos de um triângulo retângulo, aquele que possui um dos ângulos iguais a 90°. Essas métricas são chamadas, pela matemática, de funções trigonométricas.

Leis trigonométricas – Como calcular seno cosseno e tangente?

Para identificar onde se localizam e como calcular cada uma das funções trigonométricas (seno, cosseno e tangente), é preciso, primeiramente, entender a denominação de cada medida do triângulo retângulo.

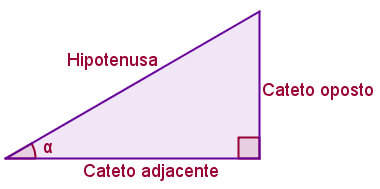
Tem-se o cateto oposto (sempre a direita do ângulo), o cateto adjacente (sempre à direita do ângulo) e a hipotenusa (diagonal). Para saber onde fica cada um deles, é preciso considerar sempre um ângulo como referência, sendo que o cateto oposto, como já diz o nome, tem que estar sempre ao oposto do  ângulo base e o cateto adjacente, que está com a  linha encostando no ângulo de referência.

Seno (Sen)

O Seno é o resultado da divisão entre o cateto oposto e a hipotenusa. Esse cálculo é definido pela lei dos senos.

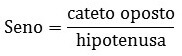
Cosseno (Cos)

O cosseno é definido pela razão entre o cateto adjacente e a hipotenusa, cálculo pré-determinado pela lei dos cossenos.

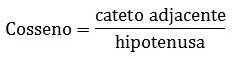
Tangente

É calculada por meio da divisão entre o cateto oposto e o cateto adjacente, servindo somente para triângulos retângulos.

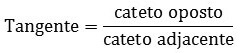
Tabela

Para não precisar calcular o seno, o cosseno e a tangente sempre que houver uma função trigonométrica, existe a tabela da trigonometria, a qual define o valor correto de cada uma das medidas do triângulo, de acordo com o grau de seu ângulo.

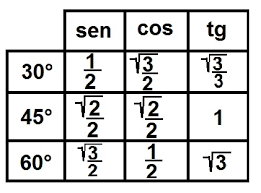
Há quem prefira decorar a tabela trigonométrica com a ajuda de músicas, como no exemplo, abaixo, com uma paródia da canção natalina Jingle Bells.

Exercícios de trigonometria com gabarito

A trigonometria é uma parte importante da matemática, uma vez que, ao conseguir calcular o lado de um triângulo, é possível descobrir a área de espaços, o que pode ser útil em navegações, astronomia, topografia, cartografia e diversas outras ciências.

Aprenda a calcular funções trigonométricas com os exemplos em passo a passo, abaixo:

1) (UFPI) Um avião decola, percorrendo uma trajetória retilínea, formando, com o solo, um ângulo de 30°. Depois de percorrer mil metros, qual será a altura atingida pelo avião?

1. Identifica-se os valores da equação trigonométrica. Sabemos que o seno é de 30° e a altura de mil metros, portanto, queremos saber a tangente;
2. Aplica-se os valores na equação sen 30º 0 x/1000;
3. Resolve-se a equação:1/2 = x/1000
   2 x = 1000
   x= 500
4. Tem-se o resultado: a altura do avião será de 500 metros.

2)  (CEFET-MG) Uma escada de 6m está apoiada numa parede. Sobre ela, forma-se um ângulo em que a distância do ponto de apoio do solo até a parede é de:

1. Identifica-se os valores da questão, sendo a tangente do triângulo de 6 metros, queremos saber o cosseno;
2. Aplica-se a lei dos cossenos, utilizando a tabela trigonométrica: cos ɑ = √5
   3
3. Resolve-se a equação: cos ɑ = x
   6
   √5 = x
   3    6
   3x = 6.√5
   x = √5
   3
   x = 2√5
4. Tem-se o resultado: a distância do ponto de apoio até a parede é de, aproximadamente, 2√5.

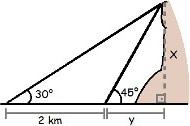
3)  (UFMG) Ao chegar perto de uma ilha, o capitão de um navio avistou uma montanha e quis medir sua altura. Ele mediu um ângulo de 30° em direção ao cume. Depois de navegar mais de 2km em direção ao morro, ele repetiu o procedimento e constatou um ângulo de 45°. Utilizando √3 = 1,73, qual é o valor que mais se aproxima da distância dessa montanha, em quilômetros?

1. Ilustra-se a situação para identificar os valores da equação:
   
2. Vê-se que o que queremos descobrir é o valor da tangente, o que, conforme a lei, é a divisão entre o cateto oposto pelo cateto adjacente. Sabemos, também, que a tangente de 45° é igual a 1 e a tangente de 30° é o mesmo que a raiz de três. Por isso, temos: tg 45° = x → x = tg 45°.y
   tg 30° = x → x = tg 30°.(2+ y)
   2 + y
3. Agora, devemos igualar os termos e resolver a equação: tg 45° . y = tg 30° . (2 + y)
   y = √3 . (2 + y)
   y = 1,73 . (2 + y)
   3y = 1,73y + 3,46
   3 y – 1,73y = 3,46
   1,27y = 3,46
   y = 3,46
   1,27
   y = 2,7 km
4. Por fim, encontramos o valor de y, mas o que queremos saber é o de x, por isso, agora podemos calcular a tangente de 45°, vezes o valor de y:x = tg 45°. y
   x = 1 . 2,7
   x = 2,7 km
5. Temos o resultado: a montanha mede, aproximadamente, 2,7 quilômetros de altura.