Pirâmide – Características, Propriedades e Medidas
Pirâmides são formas tridimensionais bastante conhecidas e apreciadas por arquitetos. Podem ser encontradas em construções antigas no Egito, na América Central (México e Guatemala) e no Oriente.
Características da Pirâmide
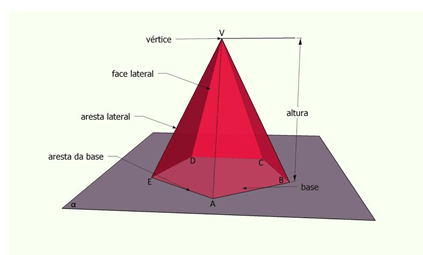
As pirâmides possuem duas características: a base é um polígono e as faces laterais são triangulares. Formalmente, elas podem ser definidas como sendo uma figura geométrica formada pela reunião de todos os segmentos de reta, que têm uma extremidade no ponto V e a outra num ponto do polígono P, como mostra a figura, abaixo.
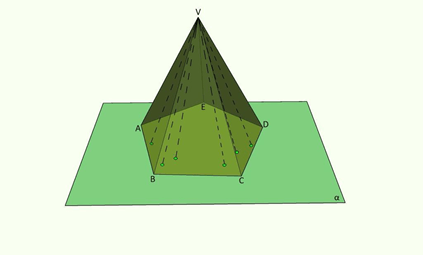
Ademais, numa pirâmide, convém destacar os seguintes elementos:

Propriedades da pirâmide
Uma pirâmide recebe denominação de acordo com o polígono da base, por exemplo: triangular, se sua base é um triângulo; quadrangular, se sua base é um quadrilátero; pentagonal, se sua base é um pentágono; etc.
Pirâmide regular
Uma pirâmide é regular se sua base é um polígono regular e o segmento que une o vértice V da pirâmide ao centro da base é perpendicular à base.
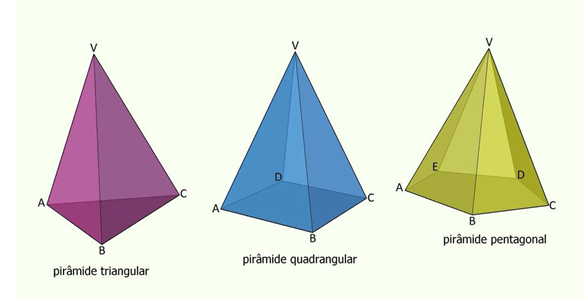
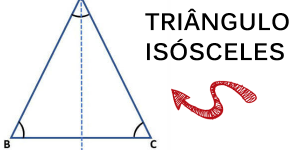
Em uma pirâmide regular, as arestas laterais são congruentes entre si e as faces laterais são triângulos isósceles congruentes entre si.
Áreas da superfície de uma pirâmide
Todos os prismas e as pirâmides podem ser representados por uma planificação. Informalmente, planificar um poliedro consiste em estender a sua superfície em um plano. Ou seja, fazer um “molde” para o sólido, de modo que cada face fique ligada a, pelo menos, uma outra por uma aresta.
A ideia é calcular separadamente a área de cada uma das figuras obtidas após a planificação para determinar a área lateral e a total.
Exemplo
Vamos calcular a área da base, a área lateral e a área total de uma pirâmide regular quadrangular, na qual a aresta da base mede 6cm e a altura da base mede 4cm.
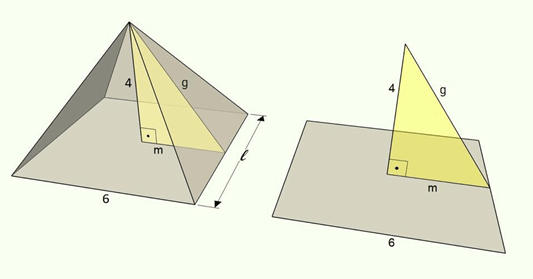
Como a base é quadrada, área da base é dada por:
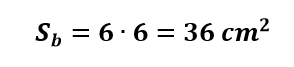
Para encontrar a área lateral, temos que determinar, primeiramente, o valor de g. Usando o Teorema de Pitágoras, e considerando que m = 3, obtemos que:
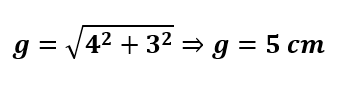
A área lateral (Sl) é quatro vezes a área de uma das faces triangular, portanto, a área total é a área lateral mais a área da base, ou seja:
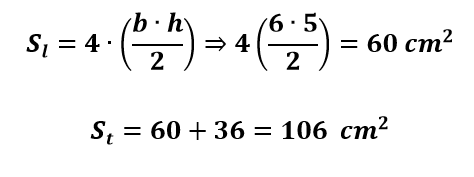
Volume de uma pirâmide de base qualquer
O volume de qualquer pirâmide é igual a um terço do produto da área de sua base pela medida de sua altura, ou seja:
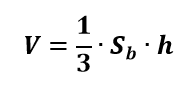
Exemplo
Em uma pirâmide regular de base quadrada, a área da base mede 16cm2 e a altura 8cm. Qual o volume da pirâmide?
Resolução
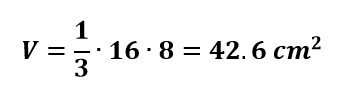
Seção de uma pirâmide
A interseção de uma pirâmide com um plano que intercepta todas as arestas laterais denomina-se secção da pirâmide, como mostra a seguinte figura:
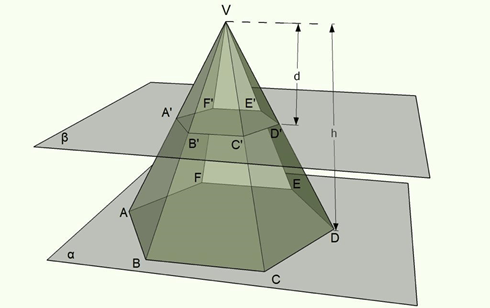
A secção determinada numa pirâmide por um plano paralelo à base é denominada secção transversal. A partir dela, podemos estudar o volume do tronco de uma pirâmide.
Volume do tronco de pirâmide
Consideremos o tronco de pirâmide representado pela seguinte figura:
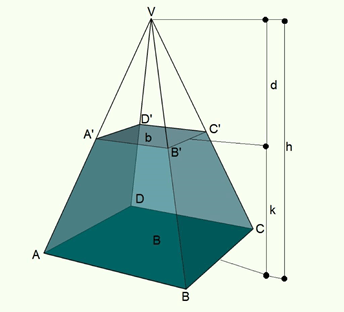
Nesse caso, a fórmula do volume do troco de uma pirâmide é:

Exemplo:
É dado um tronco de pirâmide regular, cujas bases são quadrados de lados l = 16m e l’ = 6m. A altura de uma face lateral do tronco mede 13m. Calcular o volume desse tronco:
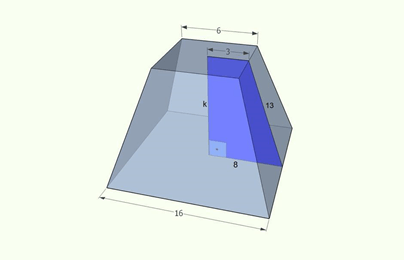
A área da base maior (B) é dada por: B = 16 . 16 = 256m2.
A área da base menor (b) é dada por: b = 6 . 6 = 36m2.
Para determinar a altura k, temos que usar o Teorema de Pitágoras de tal modo que:
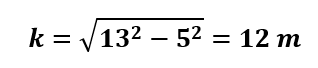
Substituindo os valores de B, b e k na equação para o volume do tronco da pirâmide, teremos:
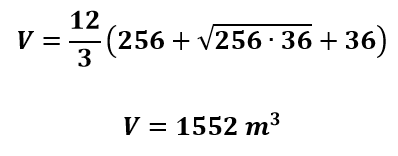







Deixe seu comentário