Paralelepípedo – Volume, Forma, Como desenhar e Exercícios

Entre os poliedros mais conhecidos, podemos destacar os prismas. Paralelepípedos são prismas cujas faces são paralelogramos e qualquer uma dessas faces serve de base.

Um paralelepípedo possui 6 faces idênticas entre si, 12 arestas e 8 vértices. Estudaremos melhor essas medidas e como calcula-las a seguir, só aqui no Gestão Educacional!

Construção e definição de prisma

Considere o plano α. Vamos imaginar uma região poligonal contida no plano α. Essa região pode ser, por exemplo, um pentágono, no qual seus vértices são os pontos ABCDE, também contidos no plano α (o plano formado por esses pontos já foi definido anteriormente como contido no plano, consequentemente, eles estão contidos no plano α).

Agora, escolha um ponto A’ e, a partir desse ponto, trace um plano β paralelo ao plano α. Forme o segmento de reta AA’, de modo que ele faça um ângulo reto com o plano α.

Agora, trace seguimentos paralelos a AA’, utilizando os pontos B, C, D e E. Esses seguimentos devem ter, em uma das extremidades, os pontos A, B, C, D e E, e chamaremos os pontos das outras extremidades de B’, C’, D’ e E’, como mostra a imagem abaixo.

Esses novos segmentos são, portanto, paralelos entre si.

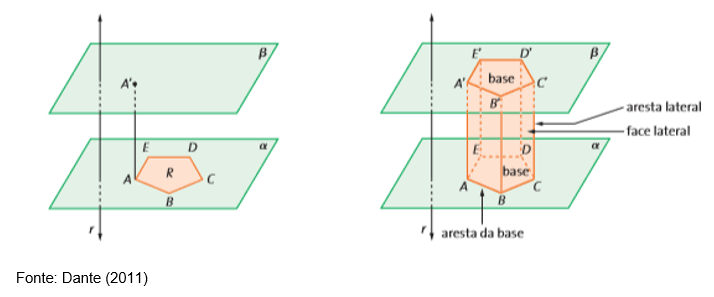
O quadrilátero formado pelos pontos AA’B’B é plano, pois seus lados AA’ e BB’ são paralelos. Os segmentos AB E A’B’ são paralelos também, porque estão contidos em dois planos paralelos. Logo, o quadrilátero AA’B’B é um paralelogramo.

Isso se repete para os quadriláteros BB’C’C, CC’D’D, e assim por diante, sendo então todos paralelogramos.

As regiões limitadas por paralelogramos e pelas regiões poligonais ABCD e A’B’C’D’ formam um poliedro chamado prisma.

Observe na imagem quais são as faces laterais, as arestas laterais e as arestas da base – iremos utilizar todos esses conceitos adiante.

Caso particular do prisma: paralelepípedo

Quando as bases (regiões poligonais) forem paralelogramos (como os da imagem abaixo), temos um prisma particular chamado paralelepípedo.

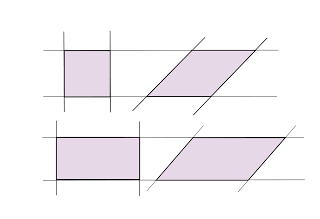
Lembre-se: retângulo é um caso particular de paralelogramo.

Se todo quadrado é um retângulo e todo retângulo é um paralelogramo, podemos concluir que todo quadrado é um paralelogramo.

Por isso, podemos sim dizer que todas as figuras acima em lilás são paralelogramos.

Definindo paralelepípedos

Paralelepípedos são prismas cuja particularidade é que qualquer uma de suas faces pode ser tomada como base, pois duas faces opostas quaisquer estão situadas em planos paralelos e são ligadas por arestas paralelas entre si (DANTE, 2011).

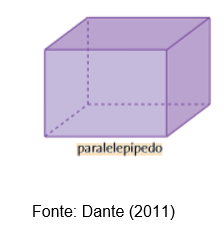Dica: todo cubo é paralelepípedo, mas nem todo paralelepípedo é cubo.

[ENTENDA MAIS SOBRE O QUE É UM CUBO E QUAIS AS SUAS MEDIDAS, AQUI!]

Paralelepípedo reto e oblíquo

Dizemos que um prisma é reto quando as arestas laterais são perpendiculares às bases. Por outro lado, dizemos que é oblíquo quando não o são.

Assim, em um prisma reto, as faces laterais são regiões retangulares.

Dito isso, podemos concluir que, quando o prisma é reto e a base é uma região retangular, obtemos um paralelepípedo retângulo ou bloco retangular.

Portanto, fica definido que paralelepípedo reto é aquele em que as arestas laterais são perpendiculares às bases. Por outro lado, paralelepípedos oblíquos são aqueles em que essa situação não ocorre.

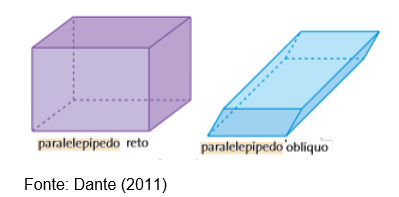
Outra conclusão que podemos tirar é que cada face do paralelepípedo retângulo é uma região retangular.

Calculo da diagonal de um paralelepípedo retângulo

Observe a figura a seguir, que apresenta um paralelepípedo retângulo.

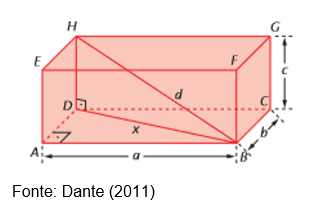Perceba que ele possui dimensões de valores a, b e c. Além disso, d é medida da diagonal do paralelepípedo e x é medida da diagonal da base.

Se você observar a figura, irá perceber a presenta de dois triângulos retângulos, ΔABD e ΔDHB, como mostra a figura:

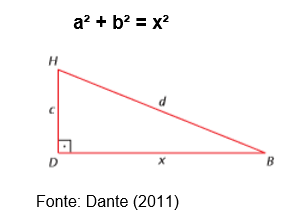
Nesse primeiro triangulo, pelo Teorema de Pitágoras, podemos fazer:

Agora, observando o segundo triangulo, podemos fazer: d² = x² + c².

Substituindo x² nessa última equação por (a² + b²), teremos: d² = (a² + b²) + c², ou:

Área da superfície de um paralelepípedo

Para calcular a área total de um paralelepípedo retângulo como o da imagem, faremos:

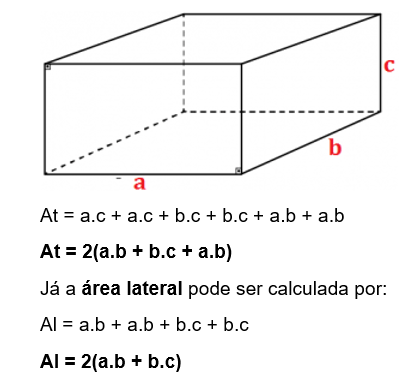
Volume do paralelepípedo

Considere um paralelepípedo de medidas a, b e c, como mostra a figura abaixo:

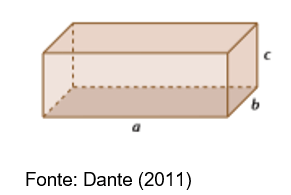
Podemos calcular, então, seu volume fazendo: V = a.b.c.

Sendo a.b = Ab (área da base), podemos escrever a fórmula acima de outra maneira: V = Ab.C, sendo c = altura (h) – V = Ab.h.

Exercícios Resolvidos

1) Uma indústria precisa fabricar 10.000 caixas de sabão com as medidas da figura abaixo. Desprezando as abas, calcule, aproximadamente, quantos metros quadrados de papelão serão necessários.

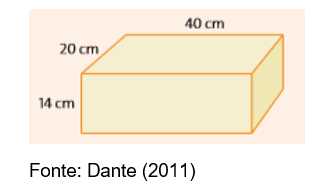
Resposta:

Sendo a área total indicada por: At = At = 2(a.b + b.c + a.b), faremos:

At =  2(40. 20 + 40. 14 + 20.14) =  2(800 + 560 + 280) = 3 280cm²

Como são 10.000 caixas, temos: A = 3 280 . 10 000 = 32 800 000cm² = 3 280 m².

2) Qual é o volume de concreto necessário para construir uma laje de 20 cm de espessura em uma sala de 3 m por 4 m?

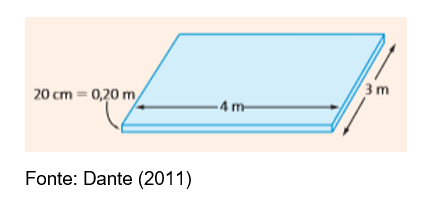
Resposta:

Área da base: Ab = 3.4 =12m²

V = área da base x altura = 12 . 0,2 = 2,4m³.