Matrizes e determinantes – O que são? Representação, Elementos, Classificação

Por Natália Alves em 19/08/2019, às 11:08

Matrizes são um grupo ordenado de números dispostos em tabelas compostas por linhas e colunas. Certas áreas da economia, como informática, logística e computação gráfica, exigem uma eficiente organização de informações, algo que é feito graças ao surgimento das matrizes.

Historicamente, a representação de conjuntos numéricos em formas de tabelas e, posteriormente, em forma de matrizes, consolidou-se no século XIX. Porém, já em 250 a.C., o livro chinês sobre arte matemática, chamado Chiu-Chang Suan-Shu, já utilizava tabelas retangulares, cujas resoluções eram feitas na forma de matriz.

O que são matrizes?

Denomina-se matriz m x n uma tabela retangular formada por m.n números reais, sendo que chamamos de m o número de linhas e n o número de colunas. Dizemos que a matriz é de ordem m x n quando colocamos primeiramente o número de linhas e depois o número de colunas, sempre nessa ordem.

Veja alguns exemplos:

A matriz abaixo possui 3 linhas e quatro colunas. Dizemos, então, que ela é de ordem 3×4.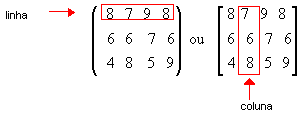

Representação de matrizes

Para representar matrizes, podemos usar:

( ) parênteses;
[ ] colchetes;
|| || barra dupla.

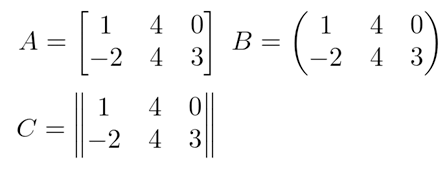Em alguns lugares, podemos ver matrizes representadas por uma barra simples, por exemplo, A = |2|, porém, essa notação não é usada para representação, e sim para o cálculo de determinantes, que é o que veremos a seguir.

Elementos de uma matriz

Podemos fazer representações genéricas de uma matriz. Os números que aparecem na matriz são chamamos de elementos ou termos da matriz.

Para representar um elemento de uma matriz, usamos a letra com dois índices: o primeiro indica em que linha o elemento se encontra, e o segundo indica em que coluna esse mesmo elemento se encontra.

Veja o seguinte exemplo: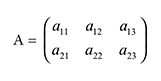A matriz acima é uma matriz A_2×3,que possui 2 linhas e três colunas. O elemento que está na linha 1 e coluna 1 é chamado de a₁₁. O elemento que está na linha 1 e coluna 2 chamamos de a₁₂. E assim continuamos escrevendo genericamente os elementos de uma matriz.

Ou seja, o elemento genérico de uma matriz A será indicado por a_ij, em que i representa a linha e j representa a coluna na qual o elemento se encontra.

Classificação de matrizes quanto ao número de linhas e colunas

Denominamos uma matriz geralmente com uma letra maiúscula.

Matriz quadrada: quando o número de linhas de uma matriz for igual ao número de colunas, m = n, diz-se que a matriz é do tipo n x n ou simplesmente de ordem n.

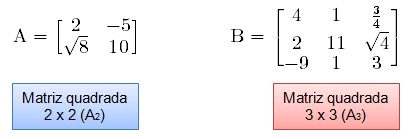Numa matriz quadrada de ordem n, os elementos a11, a22, a33… formam a diagonal principal. Portanto, os elementos da diagonal principal são os elementos a_ij_,tais que i = j.

A outra diagonal da matriz quadrada se denomina diagonal secundária. Na secundária, temos i + j = n + 1.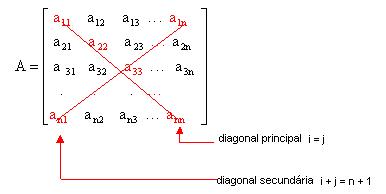

Matriz linha: quando m = 1, a matriz é chamada de matriz linha. Ou seja, ela é de ordem 1 x n, com uma única linha.

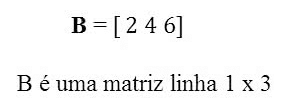
Matriz coluna: quando n = 1, a matriz é chamada de matriz coluna. Ou seja, ela é de ordem m x 1, com uma única coluna.

Nomenclatura de matrizes quanto aos seus elementos

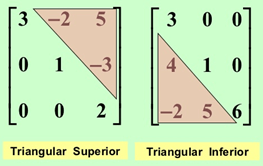
Matriz triangular: em uma matriz quadrada de ordem n, quando os elementos acima ou abaixo da diagonal principal são todos nulos, dizemos que a matriz é triangular. Em uma matriz desse tipo, aij = 0 para i > j ou i < j.

Matriz diagonal: A matriz quadrada de ordem n é chamada de matriz diagonal quando os elementos acima e abaixo da diagonal principal são nulos.

Os elementos da diagonal principal também podem ser nulos.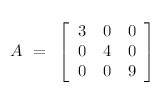

Matriz identidade: a matriz quadrada de ordem n em que todos os elementos da diagonal principal são iguais a 1 e os outros elementos são iguais a zero é chamada de matriz identidade, e seu símbolo é I_n.

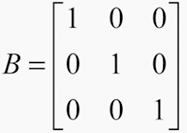
Matriz nula: a matriz que possui todos os seus elementos iguais a zero é chamada de matriz nula.

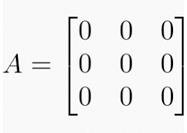
Determinantes

Existe uma notação bastante simples para o determinante de uma matriz quadrada, que é a colocação de uma barra vertical simples à esquerda e outra à direita dos elementos da matriz.

O determinante de uma matriz A é um número real indicado por det A. Calculamos o determinante de uma matriz quadrada de acordo com a sua ordem.

Determinante de uma matriz de ordem 1 é o próprio elemento – A = [a] ⇒ det A = a.

Já em uma matriz de ordem 2, calculamos o seu determinante da seguinte maneira: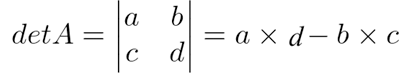Para matrizes de ordem 3, utilizamos a regra de Sarrus para calcular o determinante. Lembre-se: esse método só se aplica para matrizes de ordem 3.

Considere a matriz A quadrada de ordem 3:Copie a 1ª e a 2ª colunas no lado direito da matriz: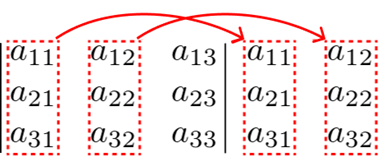Após isso, multiplicamos os termos entre si, como é indicado pelas setas abaixo. Não esqueça de colocar o sinal, como mostra a imagem: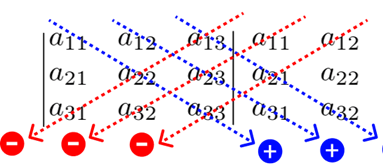Assim, o determinante da matriz A é dado por: