Cubo – O que é? Medidas, Fórmulas e Exemplos
O paralelepípedo é um prisma cujas bases são paralelogramos. Ademais, um prisma reto, cujas bases são retângulos, é chamado paralelepípedo retângulo. Esse formato é bastante utilizado na indústria de embalagens.
As principais dimensões de um paralelepípedo são: comprimento, largura e altura. Na figura abaixo, essas medidas estão representadas por 3 arestas, cujas medidas são indicadas por a, b e c respectivamente.
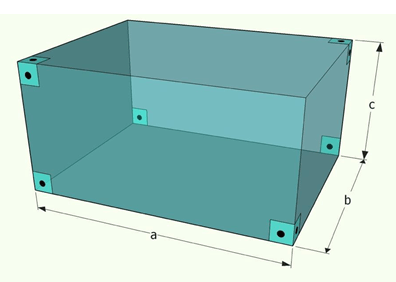
Entretanto, quando essas três dimensões são iguais, ou seja, se a = b = c, o paralelepípedo é denominado cubo. Consequentemente, como mostra figura abaixo, todas as faces são quadrados. Em nosso dia a dia, talvez o dado seja a primeira imagem que salta aos olhos quando pensamos em cubo.
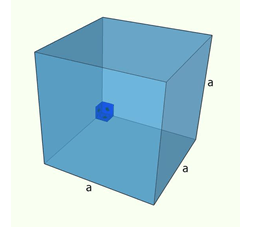
O nosso interesse é o cubo como forma geométrica, entretanto, muitas propriedades podem ser obtidas tendo como ponto de partida o paralelepípedo retângulo. Vejamos alguns exemplos detalhadamente.
Diagonal de um paralelepípedo retângulo
Considere o paralelepípedo retângulo de dimensões a, b e c.
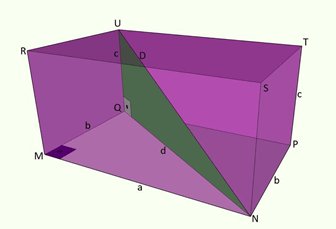
Nesse caso, a figura mostra que d e D são as medidas das diagonais da base (face MNPQ) e do paralelepípedo, respectivamente. É fácil perceber que o triângulo QMN é retângulo, então podemos determinar a diagonal da base, a partir do comprimento e da largura:
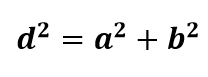
Além disso, observe que o triângulo NQU também é retângulo. Assim, usando o Teorema de Pitágoras, a diagonal do paralelepípedo é dada por:
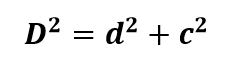
Sabendo que d2 = a2 + b2, então:
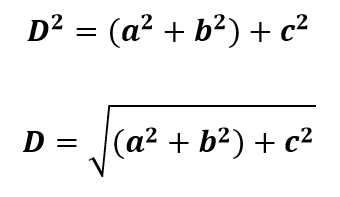
Área total de um paralelepípedo retângulo
A planificação do paralelepípedo retângulo de dimensões a, b e c é apresentada na figura, abaixo. É importante lembrar que a planificação consiste, basicamente, em desenhar uma figura tridimensional em duas dimensões (bidimensional), ou seja, todas as superfícies da figura são apresentadas em um único plano.
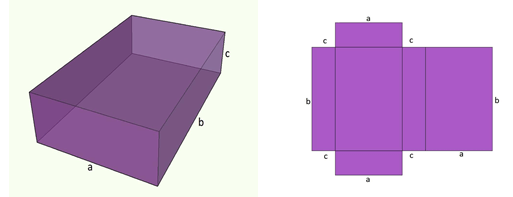
A partir dessa figura, observamos que a área total do paralelepípedo retângulo é igual à soma de todas as áreas dos seis retângulos obtidos após a planificação:
- Dois retângulos de dimensões a e b : S1 = ab;
- Dois retângulos de dimensões a e c : S2 = ac;
- Dois retângulos de dimensões b e c : S3 = bc.
Então, St = S1 + S2 + S3 – St = Sab + 2ac + bc, ou seja,
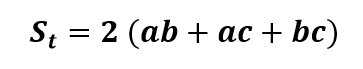
Calculo da diagonal e da área total de um cubo
Como o cubo é um caso particular do paralelepípedo, basta considerarmos todas as arestas iguais. Assim:

A diagonal da face é dada por:
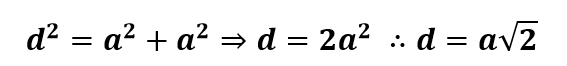 A diagonal do cubo é dada por:
A diagonal do cubo é dada por:
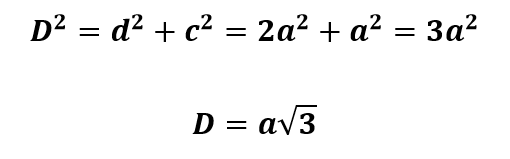
Da mesma maneira, a área total será dada por:
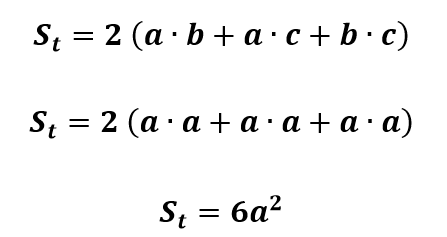
Obtemos até aqui três fórmulas importantes para o cubo. Vejamos um exemplo.
Exemplo
Dado um cubo de aresta 8cm, calcule:
- A medida da diagonal do cubo;
- A área total do cubo.
Resolução
a) A diagonal do cubo é dada por:
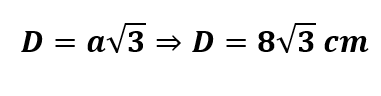 b) A área total do cubo é dada por:
b) A área total do cubo é dada por:
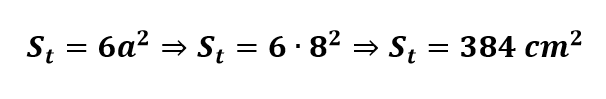
Volume de um paralelepípedo
Assim como podemos medir o comprimento de uma mesa, a superfície de uma sala, o ângulo de abertura de um compasso, a massa de uma pessoa ou a temperatura de um ambiente, também podemos medir o espaço ocupado por um objeto, um sólido geométrico. A medida do espaço ocupado por um corpo é chamada volume.
O volume de paralelepípedo pode ser obtido multiplicando-se as três dimensões do paralelepípedo: comprimento, largura e altura. Em outros termos: V = abc.
Novamente, no caso particular do cubo, é dado por: V = a . a . a – V = a3.
Note que, caso a aresta seja duplicada, formando um cubo de aresta 2a, o seu volume será 8 vezes maior que o inicial, pois: V = (2a)3 – V = 8ª3.
Não podemos esquecer que, para calcular o volume, as dimensões devem estar na mesma unidade de medida. Além disso, entre as unidades de medida de volume mais utilizadas estão o centímetro cúbico (cm3), o decímetro cúbico (dm2) e o metro cúbico (m3).
Exemplo
Um sólido de madeira tem aresta igual a 8cm. Sabendo que a densidade da madeira é 0,8g/cm3, calcule a massa desse sólido.
Resolução
O primeiro passo para resolver esse exercício consiste em encontrar o volume do sólido:
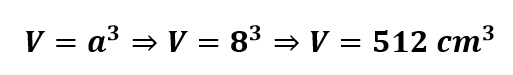
Lembrando que a densidade, o volume e a massa estão relacionadas a partir da seguinte fórmula: d = m/V.
Podemos obter a massa fazendo:
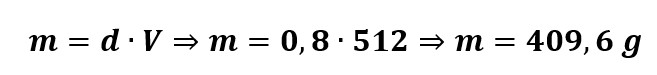
Uma caixa d’água de forma cúbica tem 3m de aresta interior. Sabendo que 1 dm3 = 1 l, qual a capacidade em litros desta caixa?
Resolução
Sabemos que 1m corresponde a 10 decímetro. Portanto, a aresta interior tem 30dm. O volume é dado por:
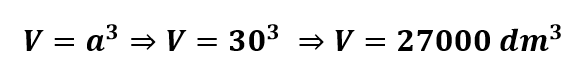
Sabendo que 1 dm3 = 1 l, então, o volume em listro é 27000 l.









Deixe seu comentário