Conjuntos numéricos – Representação, Operações, Propriedades e Exercícios

Conjuntos numéricos são agrupamentos de elementos que possuem características semelhantes, ou seja, é uma coleção de quaisquer objetos.

Por exemplo, se fizermos um conjunto com os estados da região Sudeste, teremos S = {São Paulo, Rio de Janeiro, Minas Gerais, Espirito Santo}.

Noções de conjunto

Um conjunto é formado por elementos. Esses elementos podem ser tanto um objeto quanto um outro conjunto. Por exemplo, um objeto “a” qualquer pode ser elemento de um determinado conjunto A.

Caso seja, dizemos que “a” pertence a A, portanto escrevemos a ∈ A. Caso contrário, dizemos que a não pertence a A, escrevemos a ∉ A

Representação de um conjunto

Podemos representar um conjunto de 3 formas:

1) Citação ou enumeração dos seus elementos:

Um conjunto pode ser representado por uma letra maiúscula e tem seus elementos envolvidos por chaves e separados por vírgula. Por exemplo A = {1, 2, 3, 4}

2) Propriedade ou condição:

Seja a propriedade p: x é um número par menor que 5 e maior que 0. O conjunto então será I = {2, 4}.

3) Diagramas:

O diagrama de Euler-Venn é um exemplo de representação, como mostra a figura:

Conjuntos vazio, unitário, finito, infinito e universo

A notação para o conjunto vazio é dada por Ø ou {  }, que é um conjunto que não possui elementos. Um exemplo desse conjunto pode ser:

• A = {X|X é um número natural ímpar menor que 1} = Ø. Isso ocorre porque não existem números naturais ímpares menores que 1.

O conjunto unitário é aquele formado por um único elemento, por exemplo, A = {2}. Perceba: Ø é diferente de {Ø}, pois {Ø} é um conjunto unitário que tem como único elemento o conjunto vazio.

Conjuntos finitos são aqueles que possuem uma quantidade determinada de elementos, por exemplo, o conjunto dos estados brasileiros.

Por outro lado, conjuntos infinitos são aqueles que não podemos estabelecer a sua quantidade de elementos, como o conjunto dos números pares positivos B = {2, 4, 6, …}.

Por último, temos o conjunto universo, cuja notação é U. Esse conjunto representa todos os elementos que estamos trabalhando em um determinado momento, ou seja, ao determinarmos o universo U, todos os elementos pertencem a U e todos os conjuntos são partes de U.

Por exemplo, se U é o conjunto dos números naturais, x + 7 = 2 não teria solução, porém se U for o conjunto dos números reais, temos que a solução é x = -5.

Subconjunto e relação de inclusão

Vamos considerar nesse exemplo os conjuntos A e B. Se todos os elementos do conjunto A estiverem presentes também no conjunto B, podemos afirmar que A está contido em B, ou seja, A subconjunto de B.

Teremos, então, que A ⊂ B.

Caso exista um único elemento de A que não esteja também em B, dizemos que A Ȼ B.

• Propriedades da Inclusão:

1. Propriedade Reflexiva: A ⊂ A;
2. Propriedade Antissimétrica: se A⊂B E B⊂A, então A=B;
3. Propriedade Transitiva: A⊂B E B⊂C, então A⊂C.

Além disso, é importante sabermos que Ø está contido em todos os conjuntos.

Igualdade de conjuntos

Dizemos que dois conjuntos A e B são iguais se seus elementos forem os mesmos, ou seja, todos os elementos que estão em A também estão em B.

Conjunto das partes

O Conjunto das partes mostra quais são todos os subconjuntos de um conjunto qualquer. Vamos analisar o conjunto A = {a, b, c}.

O conjunto das parte de A será: P(A) = {Ø, {a}, {b}, {c}, {a,b}, {a,c}, {c,d}, {a,b,c}}

Portanto, podemos concluir que se A tem n elementos, P(A) terá 2^(n) elementos.

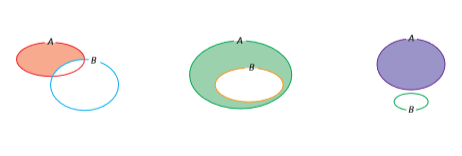
União de conjuntos

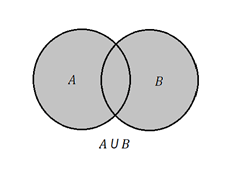
Dados os conjuntos A e B, dizemos que a união de A e B é o conjunto formado por todos os elementos de A mais os elementos de B.

De modo geral, podemos escrever: A ∪ B = {X|X∈A ou X∈B}.

Por exemplo, se A = {2,3} e B = {3,5,7}, A∪ B = {2, 3, 5, 7}.

No diagrama abaixo, a união está representada por toda a parte pintada de cinza:

Intersecção de conjuntos

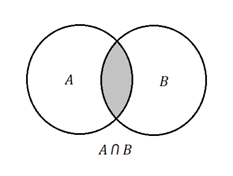
Dados os conjuntos A e B, a intersecção de dois conjuntos representa todos os elementos que estão no conjunto A e também estão no conjunto B.

De modo geral, podemos escrever: A ∩ B = {x|x ∈ A e x ∈ B}. 

Por exemplo, se A = {2, 4, 6} e B = {2, 3, 4, 5}, então A ∩  B = {2, 4}.

No diagrama, a parte pintada em cinza representa essa intersecção.

Propriedades da união e da intersecção

Dados três conjuntos, A, B e C, valem as propriedades:

1) A ∪ B = B ∪ A

A ∩ B = B ∩ A (comutativa)

2) (A ∪ B) ∪ C = A ∪ (B ∪ C)

(A ∩ B) ∩ C = A ∩ (B ∩ C) (associativa)

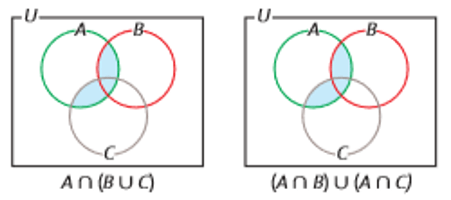
3) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) (distributiva)

 

 

 

 

 

 

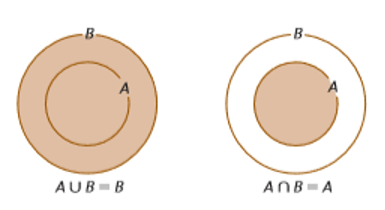
4) A ⊂ B é ⇔ A ∪ B = B ⇔ A ∩ B = A

 

 

 

 

 

 

5)A ⊂ B ⇒ (A ∪ C) ⊂ (B ∪  C)

A ⊂ B ⇒ (A ∩  C) ⊂  (B ∩ C)

Diferença de conjuntos

Dados os conjuntos A = {0, 1, 3, 6, 8, 9} e B = {1, 4, 9, 90}, podemos escrever o conjunto C formado pelos elementos que pertencem a A, mas que não pertencem a B. Portanto, C = {0, 3, 6, 8}.

O conjunto C é chamado diferença entre A e B e é indicado por A – B (lê-se A menos B).

De modo geral, escrevemos: A-B = {X|X ∈ A e X ∉ B}

Número de elementos da união de conjuntos

De modo geral, quando A e B são conjuntos finitos, tem-se:

N (A U B) = n(A) + n(B) – n(A ∩ B), quando A ∩ B ≠ ∅

No caso de 3 conjuntos, teremos:

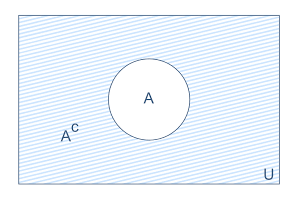
Complementar de um conjunto

Dado um universo U e um conjunto A, dizemos que o complementar de A em relação a U é o conjunto de todos os elementos de U que não pertencem a A. Indica-se:

E, de modo geral, podemos dizer que:

O diagrama da situação descrita está abaixo:

Exercícios Resolvidos

1) Dados os conjuntos A = {1, 2, {3, 4}, {5}} verifique se os itens abaixo são verdadeiros ou falsos.

A) (3,4} ⊂ A

B) {5} ⊂ A

C) {5} ∈A

D) 1 ⊂ A

Respostas:

A) Falso

B) Falso

C) Verdadeiro

D) Falso

2) Indique simbolicamente a parte colorida no diagrama:

 

 

 

 

 

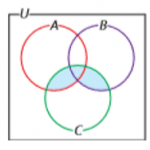
Resposta: (A U B) ∩ C