O que são função bijetora, sobrejetora e injetora? Exemplos!

O conceito de função é um dos mais importantes da Matemática e ocupa lugar de destaque em vários de seus campos de estudo, bem como em outras áreas do conhecimento. É muito comum e conveniente expressar fenômenos físicos, biológicos, sociais etc. por meio de funções.

Dizemos que uma função é injetora quando o domínio possui elementos correspondentes distintos no contradomínio. Já uma função é sobrejetora quando sua imagem é igual ao seu contradomínio. Por fim, é bijetora uma função ao ser sobrejetora e injetora ao mesmo tempo.

O que é uma função?

Dados dois conjuntos não vazios, A e B, uma função de A em B é uma regra que indica como associar cada elemento x ∈ A a um elemento y ∈ B.

Usamos a seguinte notação: f: A → B (lê-se: f é uma função de A em B).

A função f transforma x de A em y de B.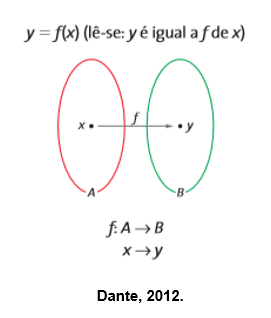Dada uma função f de A em B, o conjunto A chama-se domínio da função (D) e o conjunto B contradomínio (CD) da função.

O valor assumido pela função f para x ∈ A chama-se imagem de x pela função f. O conjunto de todos os y assim obtidos é chamado conjunto imagem da função f, e é indicado por Im(f).

Por exemplo, a função f(x) = x² f transforma cada número real x em outro número real y, que é o quadrado de x.

O conjunto imagem é Im(f) = R₊, o domínio é D(f) = R e o contradomínio é CD = R.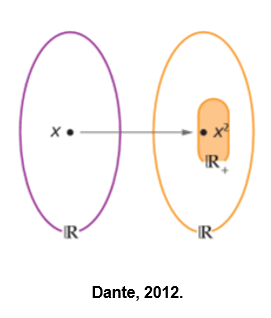

O que é uma função injetora?

Também chamada de função injetiva, uma função é injetora quando não há elemento do contradomínio que seja imagem de mais de um elemento do domínio.

Ou seja, elementos diferentes do domínio são transformados por f em elementos diferentes da imagem.

Portanto: f(x1) = f(x2) ⇔ x1 = x2

Observe os seguintes exemplos:

1) A função f(x) = x² não é injetora, pois:

• Para x = 2, f(2) = 4;
• Para x = -2, f(-2) = 4.

Ou seja, se y = 4, temos que x = 2 ou x = -2. Nesse caso, existem dois elementos do domínio (2 e –2) que resultam em um valor de imagem (4). Portanto, essa função não é injetora.

2) Já a função f(x) = 2x + 2 é injetora, pois corresponde a cada número real x o seu dobro 2x, e não existem dois números reais diferentes que tenham o mesmo dobro. Ou seja, não existe dois elementos do domínio que correspondam a um único elemento na imagem da função.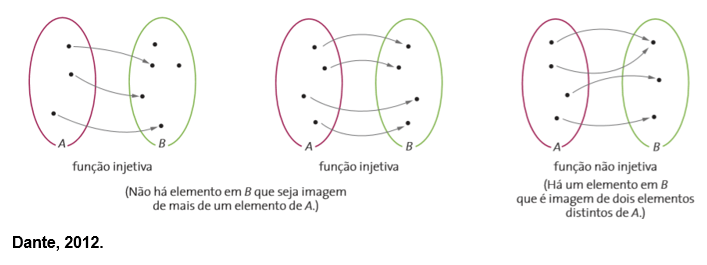

Podemos verificar se uma função é injetora olhando seu gráfico. Sabemos que, se a função é injetora, não há elemento da Im(f) que seja imagem de mais de um elemento do domínio. Assim, imaginando linhas horizontais cortando o gráfico, elas só podem cruzar uma única vez para cada valor de y.

Caso as linhas horizontais intersectam o gráfico mais de uma vez. A função não é injetora.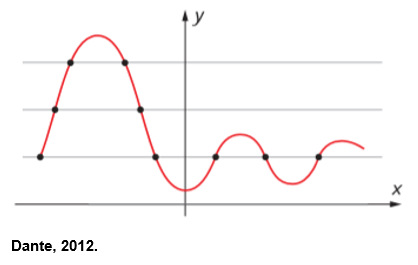Porém, se as linhas horizontais nunca intersectam o gráfico mais de uma vez, então, a função é injetora.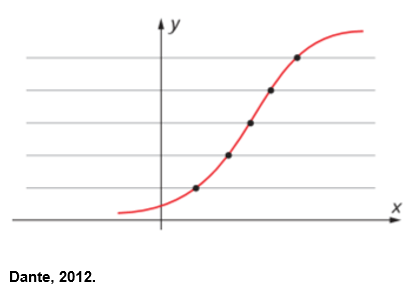

O que é uma função sobrejetora?

Também chamada de função sobrejetiva, uma função f: A → B é sobrejetora quando todo elemento de B possui pelo menos um correspondente em A, ou seja, o contradomínio é sempre igual ao conjunto imagem.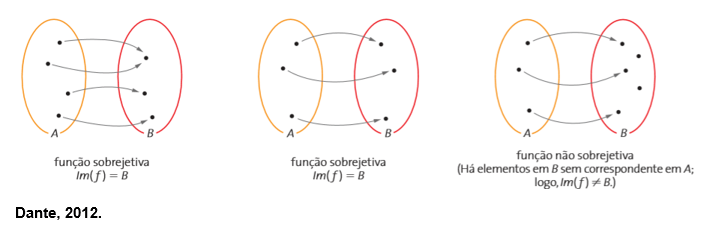

O último caso representado na imagem acima mostra uma função que não é sobrejetora. Porém, essa função é injetora, pois todos os elementos do conjunto A (domínio) possuem um único correspondente no conjunto B, não havendo importância de ter elementos em B sem nenhum correspondente em A.

A função f(x) = x² não é sobrejetora pois o conjunto imagem é Im(f) = R₊  e o contradomínio é CD = R, sendo, portanto, diferentes.

Observe que a área preenchida em laranja (imagem da função) não é igual ao conjunto B (contradomínio da função).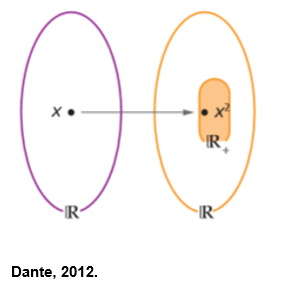

O que é uma função bijetora?

Uma função f: A → B é bijetora ou bijetiva se ela for simultaneamente injetora e sobrejetora. Quando isso ocorre, dizemos que há uma bijeção ou uma correspondência biunívoca entre A e B.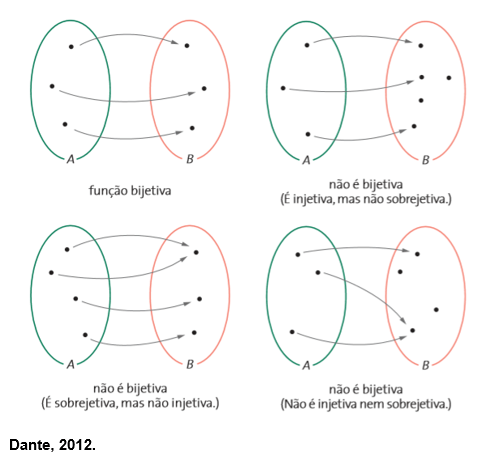Vamos analisar alguns exemplos:

1) a função f(x) = x² não é bijetiva, pois, embora seja sobrejetiva, ela não é injetiva.

2) a função f(x) = x + 1 é bijetiva, pois é sobrejetiva e injetiva.