Queda livre – O que é? Fórmulas, Exemplos e Exercícios
A queda livre é todo movimento vertical sob ação da gravidade, sendo classificado como retilíneo e uniformemente variado. Quando um objeto é solto de determinada altura, adquire um movimento de queda em trajetória vertical, tendo sua velocidade aumenta conforte o tempo, devido à aceleração gravitacional, cujo valor é, aproximadamente, g = 9,8 m/s².
Galileu subiu ao topo da Torre de Pisa (a torre que conhecemos por ser inclinada) e deixou cair dois objetos: um mais leve e um mais pesado. Eles tocaram o solo ao mesmo tempo. Ele percebeu, então, que a velocidade dos corpos em queda livre não depende do peso dos corpos que caem. Se tirarmos o ar de um ambiente, ou seja, fazer com que tenha apenas vácuo ali, uma pena e uma bola de boliche levarão o mesmo tempo para cair. Portanto, na queda livre, todos os corpos têm trajetória retilínea, vertical e com a mesma aceleração: a gravidade.
O que é queda livre?
Se formos rigorosos, o movimento em queda livre não existe na prática porque dificilmente conseguimos evitar a influência da resistência do ar. Mas, podemos considerar queda livre, com boa aproximação, com o movimento de uma pequena esfera de aço.
No movimento em queda livre, a trajetória é retilínea e a aceleração constante. Portanto, é um MRUV.
Podemos reescrever as funções do MRUV para o movimento em queda livre da seguinte maneira:
- Função da velocidade em relação ao tempo:
- Função da posição em relação ao tempo:
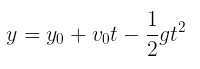
- Função da velocidade em relação à posição (Torricelli):
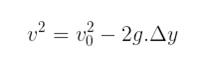
Podemos entender melhor quais são as diferenças das equações acima das equações tradicionais do MRUV, com os tópicos abaixo:
- Como a trajetória é sempre na vertical, não usamos mais a variável x para representar a posição do objeto. Portanto, agora, a posição do objeto em queda livre fica associada à variável y, relacionada ao eixo vertical das ordenadas;
- A aceleração sempre será a gravidade. Portanto, perceba que em todas as equações acima usamos a = g. Como a aceleração da gravidade é orientada sempre para baixo, o seu valor será negativo. Perceba que alguns sinais foram trocados;
- O deslocamento no MRUV é dado por Δx = x – x0. Porém, agora na queda livre, esse deslocamento será substituído pela altura h ou por Δy = y – y
Exercícios resolvidos
1) Um corpo é abandonado de uma altura de 125m. Desprezando a resistência do ar e admitindo g = 10 m/s², determine:
A) A função da posição.
B) A posição nos instantes t = 0, t = 1 e t = 2.
C) A função da velocidade.
D) A velocidade nos instantes t = 0, t = 1 e t = 2.
E) O instante em que o corpo atinge o solo.
F) A velocidade na qual o corpo atinge o solo.
RESPOSTA:
A) Posicionando o sistema de referência no solo, a posição inicial será a altura que ele foi abandonado: y0 = 125 m.
Como o corpo foi abandonado, sua velocidade inicial será zero: v0 = 0.
Substituindo esses valores na função da posição, temos: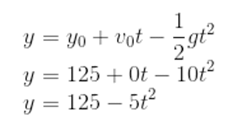 B) Substituindo os valores de t nessa função:
B) Substituindo os valores de t nessa função:
Y = 125 – 5t²
Y1 = 125 – 5.0² = 125 m
Y2 = 125 – 5.1² = 120 m
Y3 = 125 – 5.2² = 105 m
C) Sendo v0 = 0, a função velocidade será dada por: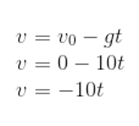 D) Substituindo os valores de t na função da velocidade:
D) Substituindo os valores de t na função da velocidade:
V1 = -10. 0 = 0 m/s²
V2 = -10. 1 = -10 m/s²
V3 = -10 . 2 = -20 m/s²
E) No instante t em que o corpo atinge o solo, de acordo com o preferencial que adotamos no início, a posição é y = 0. Então:
Y = 125 – 5t²
0 = 125 – 5t²
t² = 125
T = 5 s.
Nesse caso, a raiz de 125 nos apresenta dois valores: -5 e +5. Usamos o valor positivo (+5), pois é o único significado possível, não usamos o tempo negativo.
F) Fazendo y = 0 na função da velocidade em relação ao tempo (equação de Torricelli):
V² = v0² – 2g( y – y0)
V² = 0² – 2 . 10(0-125)
V² = 2 500
V = – 50 m/s²
Perceba que, nesse item, a raiz de 2.500 nos apresenta dois valores: -50 e +50. O sinal escolhido é o negativo, pois a velocidade é para baixo na queda livre.









Deixe seu comentário