Velocidade média – Deslocamento de tempo, Gráfico de Velocidade e Exercícios

A velocidade média é a relação da distância percorrida por um corpo num determinado espaço de tempo. A seguir, você entenderá o tipo mais simples de movimento: uma partícula se deslocando ao longo de uma linha reta.

Para descrevermos esse movimento, vamos precisar conhecer novas grandezas físicas, como a velocidade. Confira mais só aqui, no Gestão Educacional!

Deslocamento e tempo

Para estudarmos os movimentos, precisamos estabelecer um eixo de coordenadas. Vamos escolher o eixo Ox.

Para entender, observe o plano cartesiano que você está acostumado a trabalhar na escola. Vamos utilizar o eixo X para colocar as partículas em cima dele e então observar o seu movimento.

Vamos imaginar o seguinte exemplo: em uma corrida de carros, um carro percorre um trecho retilíneo, para alcançar a linha de chegada. Ou seja, ele percorre o eixo Ox desde sua origem em 0 até o ponto que quer chegar.

Vamos considerar a posição desse carro dada pela coordenada x em que ela está, que varia de acordo com o tempo que ela se move. Quanto mais tempo consideramos, mais adiante esse carro vai estar no eixo x.

Suponha que 1 segundo depois do início do movimento o carro esteja no ponto x1, a 19 metros da origem. 4 segundos depois, o carro está no ponto x2, a 277 metros da origem.

O deslocamento do carro é um vetor que aponta de x1 para x2. Podemos calcular esse deslocamento calculando a variação de x, ou seja, basta fazermos 277 – 19 = 258m.

Para calcularmos o intervalo de tempo que esse deslocamento demorou para ocorrer, basta fazermos 4 – 1 = 3 segundos.

Para calcularmos a velocidade média desse carro, iremos dividir essa variação do espaço em x pela variação de tempo: Vm = 258m / 3s = 86 m/s

Caso o carro estivesse em repouso na linha de partida, ele não teria deslocado nenhum valor e, portanto, sua velocidade seria 0.

Generalizando o conceito

Vamos generalizar o exemplo que estudamos acima. Em um instante t1, o carro se encontra no ponto de coordenada x1. No instante t2, o carro se encontra no ponto de coordenada x2.

O deslocamento do carro denominado Δx é a variação da coordenada x, ou seja, Δx = x2 – x1.

De maneira análoga, a variação do tempo, ou seja, o tempo que o carro demorou para chegar de x1 até x2, pode ser calculada por:

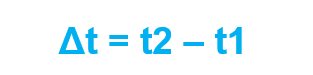
Calculamos, então, a velocidade média de símbolo Vm por:

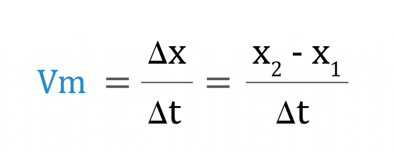
No exemplo anterior, teríamos:

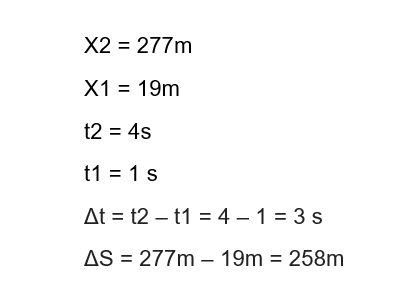
A velocidade média será:

Vm = 258 m / 3s = 86m/s.

Perceba: a unidade de medida utilizada é o m/s. Isso significa que o carro percorreu 86 metros a cada segundo que passou.

Sendo essa velocidade média positiva, durante o intervalo de tempo, o carro se move no sentido positivo do eixo, ou seja, da esquerda para a direita.

Caso o carro ou qualquer partícula se mova no sentido negativo do eixo x, sua velocidade média será negativa.

Gráfico velocidade

Há também a possibilidade de representarmos a velocidade média a partir de um gráfico do tempo pelo deslocamento, como é o exemplo abaixo:

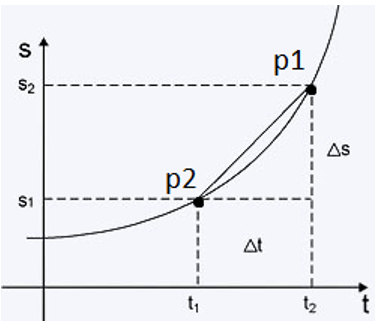
Imagine que esse gráfico descreva a trajetória daquele carro na corrida. Essa curva não representa a trajetória do carro no espaço, pois o carro anda em linha reta. Essa curva mostra a variação da posição do carro em relação ao tempo.

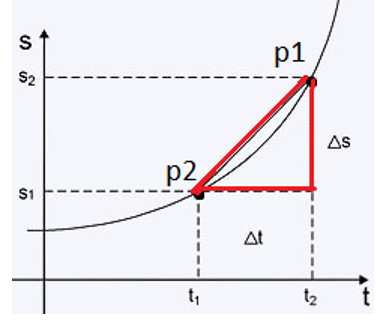
O triângulo em vermelho tem como hipotenusa a reta que liga os pontos P1 e P2. Ela é a reta que representa a velocidade média desse carro, obtida por ΔS/ ΔT.

Portanto, a velocidade média é a inclinação dessa reta que liga P1 e P2.

Isso nos leva à conclusão de que a velocidade média depende apenas do deslocamento ΔS = x2 – x1 e Δt = t2 – t1, e não dos detalhes ocorridos durante esse processo.

PERCEBA: Usar Δx ou ΔS representa a mesma coisa! São denominações diferentes para a variação distância percorrida pelo objeto. Fica a seu critério escolher qual delas usar.

Exercícios Resolvidos

1) (UECE 87.1) A velocidade de um carro, como função do tempo, pode ser descrita pelo gráfico abaixo. Qual a velocidade média do movimento?

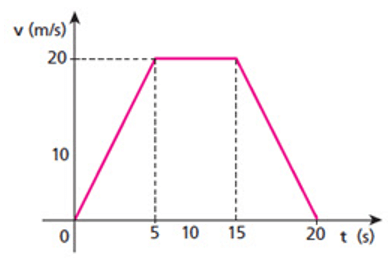
RESPOSTA: Podemos calcular a velocidade média obtendo a área abaixo da curva desse gráfico. Nesse caso, perceba que temos um trapézio, então vamos calcular a área dele.

ΔS = (B + b).h/2 = (20 + 10).20/2 = 30.10 = 300 m.

Vm = ΔS/Δt = 300/20 = 15 m/s.

2) Um motorista está percorrendo uma estrada retilínea e vê no painel de seu carro que a quilometragem que o carro percorreu até agora é de 4.000km. Ele fez uma viagem de 16 horas e, após esse período, conferiu novamente a quilometragem no visor do carro. Agora, o carro já havia percorrido 5.600km. Calcule a velocidade média em que o motorista realizou sua viagem.

RESPOSTA:

Vm = x2 – x1 / t2 – t1

Vm = 5 600 – 4 000 / 16 – 0

Vm = 1 600/16

Vm = 100 km/h

PERCEBA: A unidade de medida, nesse caso, é quilômetros por hora!