Função logarítmica – O que é? Gráfico, Fórmulas, Propriedades e Exercícios

A função logarítmica de base a f(x) = log_a x possui a real, positivo e a ≠ 1. Ela é a função inversa da função exponencial, portanto, seus gráficos são simétricos à reta x = y. A função logarítmica tem um gráfico que nunca toca o eixo Y, podemos então dizer que esse eixo é uma assíntota dessa função.

Cálculos com logaritmos estão presentes em várias atividades cotidianas. Uma delas é a medida da magnitude dos terremotos, feita pela escala Richter. Mas esse tipo de escala só foi criada graças ao matemático escocês John Napier, que formulou o logaritmo natural no século XVII, com a finalidade de simplificar os cálculos comuns da astronomia, feitos na época.

O que é logaritmo?

Dados os números reais positivos a, b e c, a ≠ 1, se b = a^c, então o expoente c chama-se logaritmo de b na base a, ou seja, log_a b = c.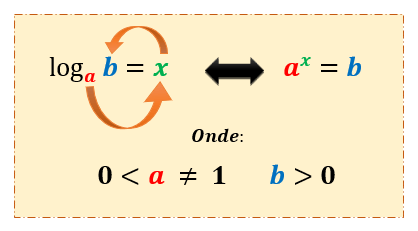Na forma logarítmica, temos log_a b = c, sendo:

• c: logaritmo;
• a: base do logaritmo;
• b: logaritmando.

Para entender melhor, podemos ver alguns exemplos:

• Log₃ 81 = 4 ⇔ 3⁴ = 81
• Log₈ 1 = 0 ⇔ 8⁰ = 1

O que é função logarítmica?

A função logarítmica associa cada número real positivo x ao número real log_a X, chamado logaritmo de x na base a, com a real, positivo e a ≠ 1.  Ela é geralmente dada por f(x) = log_a X.

O domínio da função logarítmica são os números reais positivos não nulos, e sua imagem são todos os números reais.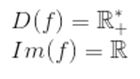As funções logarítmicas mais usadas são aquelas cuja base a é maior que 1. Particularmente, as de base 10 (logaritmos decimais), as de base 2 (logaritmos binários) e as de e (logaritmos naturais) são as que usamos com maior frequência, por facilitarem os cálculos.

As funções, abaixo, são exemplos de funções logarítmicas:

• f(x) = log₂ x
• g(x) = log _e x = ln x

Gráfico da função logarítmica

O gráfico dessa função passa pelo ponto (1,0), ou seja, f(1) = 0. O gráfico nunca toca o eixo y nem ocupa pontos dos quadrantes II e III.

Somente números positivos possuem logaritmo real, pois a função f(x) =  a^x  assume somente valores positivos. Se a > 1, os números maiores do que 1 têm logaritmo positivo, e os números compreendidos entre 0 e 1 têm logaritmo negativo. Portanto, se 0 < a < 1, os números maiores do que 1 têm logaritmo negativo, e os números compreendidos entre 0 e 1 têm logaritmo positivo.

Sabendo disso, podemos definir que:

• Quando a > 1, a função é crescente;
• Quando 0 < a < 1, a função é decrescente.

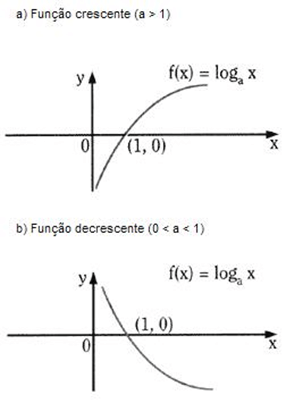A função logarítmica é ilimitada, superiormente e inferiormente. No caso de a > 1, ser ilimitada superiormente significa que se pode dar a log_a x um valor tão grande quanto se queira, desde que tomemos x suficientemente grande.

A função logarítmica é injetiva, pois números positivos diferentes têm logaritmos diferentes. Ela é também sobrejetiva, pois, dado qualquer número real b, existe sempre um único número real positivo x, tal que log_a x = b. Portanto, ela é ainda bijetiva.

Na função logarítmica f(x) = log_a x (a > 0 e a ≠ 1), sendo ela crescente ou decrescente, o eixo das ordenadas é uma assíntota vertical do gráfico, isto é, à medida que x tende para zero, o valor da função cresce ou decresce ilimitadamente, sem jamais tocar o eixo y.

A função inversa da função exponencial é a função logarítmica. Portanto, os gráficos das duas funções são simétricos à reta = x.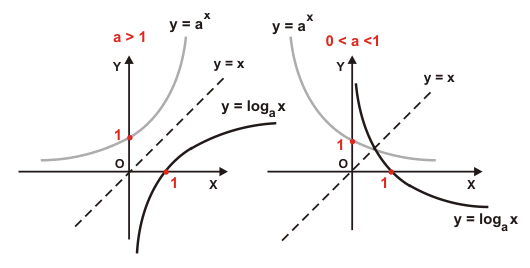

Propriedades das operações com logaritmos

Para conseguir trabalhar melhor com as funções logarítmicas, devemos relembrar algumas de suas propriedades nas operações.

Dada a definição de logaritmo, há algumas propriedades que surgem dessa definição:

log_ab = c ↔ a^c = b

Consequência da definição de logaritmo

log_a 1 = 0

log_a a = 1

log_a aⁿ = n

a^log_a^b = b

log_b a = log_bc ↔ a = b

Além disso, existem propriedades operatórias dos logaritmos, dadas por: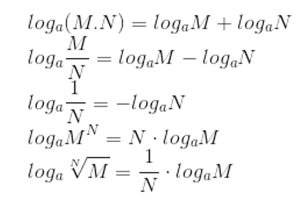Também, às vezes, é necessário trabalhar com logaritmos de bases 10, para facilitar nossas contas. Para isso, precisamos saber como funciona a mudança de base em um logaritmo: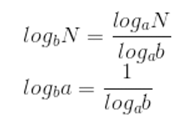

Exercício Resolvido

1) (UFSCAR – SP) A altura média do tronco de certa espécie de árvore que se destina à produção de madeira evolui, desde que é plantada, segundo o seguinte modelo matemático:

h(t) = 1,5 + log₃ (t + 1)

Com (t) em metros e t em anos. Se uma dessas árvores foi cortada quando seu tronco atingiu 3,5 metros de altura, qual foi o tempo (em anos) transcorrido do tempo de plantação ato o corte?

RESOLUÇÃO

h(t) = 1,5 + log₃ (t + 1)

3,5 = 1,5 + log₃ (t + 1)

2 = log₃ (t + 1)

t + 1 = 3²

t + 1 = 9

t = 8 anos.