Logaritmos – O que são? Definição, Nomenclatura, Propriedades e Exercícios

A construção do conhecimento científico está vinculada às necessidades sociais de cada época. O surgimento dos logaritmos ocorreu no início do século XVII, pois havia a necessidade de astrônomos, navegadores, comerciantes e engenheiros realizarem cálculos rápidos e precisos.

John Napier (1550-1617) inventou tanto a palavra quanto o conceito de logaritmo, em 1614, após estudo de vinte anos. Em seguida, essa ferramenta matemática foi sofrendo diversas mudanças.

Desde a sua invenção, há mais de 400 anos, o logaritmo ganhou importância para outras áreas, e hoje é utilizado em diversos campos da ciência, por exemplo, na Física, na Química e na Biologia.

O que é um logaritmo?

Vamos tomar como exemplo a relação entre os números 2, 4 e 16. Primeiramente, observamos que:

• Temos: 4 = 2 . 2;
• E: 16 = 4 . 4 = (2 . 2) . (2 . 2)
• Mas: 2 . 2 . 2. 2 = 2⁴
• Então, sabemos que: 16 = 2⁴

A operação que associa os números 2 e 4 (base e expoente, respectivamente) ao número 16 chama-se potenciação. Por outro lado, conhecendo a potência e a base, podemos fazer a operação inversa para encontrar o valor do expoente x tal que: 2^x = 16

A essa operação, vamos atribuir a seguinte notação: log₂ 16 = x, em que x = 4, pois 2⁴ = 16.

Essa notação é denominada logaritmação, e o número 4 é chamado logaritmo de 16 na base 2. Isso indica que log₂ (16) = 4, ou seja, 16 = 2⁴ (16 é igual a 2 elevado a 4).

Definição

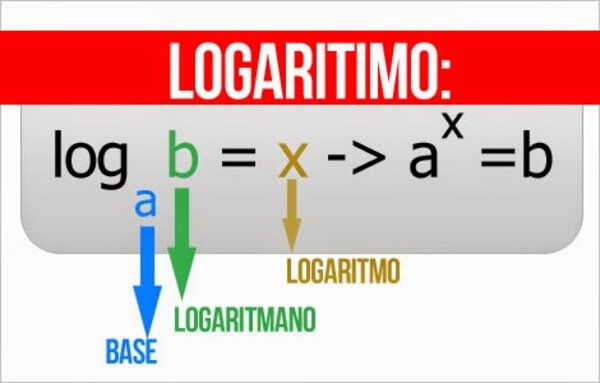
Dizemos que o logaritmo de um número positivo a, na base b, positiva e diferente de 1, é o expoente x, ao qual a se deve elevar b para se obter a – log_ba = x – b^x = a

Nomenclatura

Antilogaritmo ou logaritmando é o número a. Base é o número b. Logaritmo é o número . Sendo log_b (a) pronunciado como o “logaritmo de a na base ”.  Além disso, se a base do logaritmo for , costuma-se omiti-la na sua representação, como mostra a equação: log₁₀b = logb (log – logaritmo decimal).

Exemplos:

• log232 = 5, pois 25 = 32;
• log3 243 = 5, pois 35 = 243;
• log 1000 = 3, pois 103 = 1000;
• log2 2 = 1, pois 21 = 2.

Exercícios resolvidos

Calcule o valor de  na igualdade log₇ 49 = x

Solução: log₇ 49 = x

Usando a definição de logaritmo, 7^x = 49, mas, 49 = 7 . 7 = 7². Portanto, 7^x = 7^2.

Essa igualdade apenas é validade se x = 2, então: log₇ 49 = 2.

Propriedades importantes

Com os logaritmos, as operações são substituídas por outras mais simples: potenciações por multiplicações, multiplicações por adições, divisões por subtrações.

Essas transformações de operações mais complicadas em outras mais simples serão apresentadas na forma de propriedades.

1^a propriedade Logaritmo de um produto

O logaritmo de um produto é igual à soma dos logaritmos dos fatores, tomados na mesma base. Em linguagem matemática, temos: log_b (a . c) = log_ba + log_bc.

Exemplo:

Sabendo que o log 2 = 0,301 e log 3 = 0,477, calcule o log 6.

Solução:

Observamos que log 6 = log (2 . 3), então, aplicando a propriedade do logaritmo de produto, temos:  log 6 = log (2^.3) = log(2) + log(3) = 0,301 + 0,477 = 0,778.

2^a propriedade Logaritmo de um quociente

O logaritmo de um quociente é igual ao logaritmo do dividendo menos o logaritmo do divisor, tomados na mesma base. Em linguagem matemática, temos:

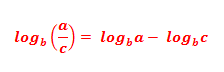
Exemplo:

Sabendo que o log 2 = 0,301 e log 3 = 0,477, calcule:

Solução:

log(2) –log(3) = 0,301 – 0,477 = -0176.

3^a propriedade Logaritmo de uma potência

O logaritmo de uma potência é igual ao produto do expoente pelo logaritmo da base da potência. Em linguagem matemática, temos: log_b aⁿ = log_ba.

Exemplo:

Sendo log 2 = 0,301, calcule log 8.

Solução:

Sabendo que 8 = 2 ^.2 ^. 2, ou seja, 8 = 2³, temos que:

log8 = log 2³ = 3^.log 2 = 3^.0,301 = 0,903

Exercícios resolvidos

A função logaritmo é uma das noções mais importantes das que integram o currículo do Ensino Médio. Vejamos duas aplicações:

1– (UFMG) O pH de uma solução aquosa é definido pela expressão pH = – log[H⁺], em que [H⁺] indica  a concentração, em mol/L, de íons de  hidrogênio na solução, e log o logaritmo na base 10.

Ao analisar uma determinada solução, um pesquisador verificou que nela a concentração de íons de hidrogênio era [H⁺] = 5,4x10^-8 mol/L.

Para calcular o pH dessa solução, ele usou os valores aproximados de 0,30, para log 2, e de 0,48, para log 3. Então, o valor que o pesquisador obteve para o pH dessa solução foi:

(a) 7,26

(b) 7,32

(c) 7,58

(d) 7,74

Solução:

É preciso usar as propriedades dos logaritmos. Acompanhe, passo a passo.

2 – (UFRJ)Seja β a altura de um som, medida em decibéis. Essa altura β está relacionada à intensidade do som I, pela expressão, abaixo, na qual a intensidade padrão I₀  é igual a 10^-12 W/m²:

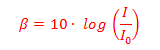
Observe a tabela, a seguir. Nela, os valores de  foram aferidos a distâncias idênticas das respectivas fontes de som:

Sabendo que há risco de danos ao ouvido médio a partir de 90 dB, o número de fontes da tabela cuja intensidade de emissão de sons está na faixa de risco é de:

(a) 1

(b) 2

(c) 3

(d) 4

Solução:

Para resolver esse exercício, é preciso determinar β para cada uma das fontes de som, usando, quando necessário, as três propriedades dos logaritmos. Além disso, temos que log (10) = 1 e log(32) = 1,5, pois log (32) = log (2⁵) = 5 . log2 = 5 . 0.3 = 1,5:

 

Os resultados mostram que a intensidade da Turbina e o Amplificador de som estão acima da faixa de risco, isto é:

Desse modo, a resposta correta é a letra b.

---

Para saber um pouco mais sobre a História dos Logaritmos, você pode ouvir os seguintes áudios:

O que é logaritmo – http://m3.ime.unicamp.br/recursos/1292

Nesse programa, o apresentador discute com um convidado especial, contando com algumas participações de ouvintes, o significado da palavra logaritmo no contexto da Matemática.

A criação dos logaritmos – http://m3.ime.unicamp.br/recursos/1279

Na aula de hoje, a professora explica a Joãozinho e Sofia como ocorreu a criação dos logaritmos e sua importância no desenvolvimento de várias áreas do conhecimento. Na segunda parte da aula, o destaque fica por conta do diálogo entre o professor Henry Briggs e o Lorde John Napier.