Geometria espacial – Características, Figuras e Cálculos
A geometria pode ser dividia em três partes: plana, espacial e analítica. A geometria espacial, especificamente, é a área da matemática que tem como objetivo estudar as figuras que possuem três dimensões.
Nessas condições as figuras são compostas por comprimento, largura e altura. Por outro lado, a geometria plana é considerada bidimensional, de tal maneira que as figuras possuem apenas Altura e Largura.
Características da Geometria espacial
Como dito anteriormente, a preocupação da geometria espacial está no estudo das figuras geométrica. Essas são conhecidas como “sólido geométricos”. Alguns exemplos são: cubo, paralelepípedo, pirâmide, cone, cilindro e esfera.
Tais figuras podem ser classificadas em dois grupos: os corpos redondos e os poliedros.
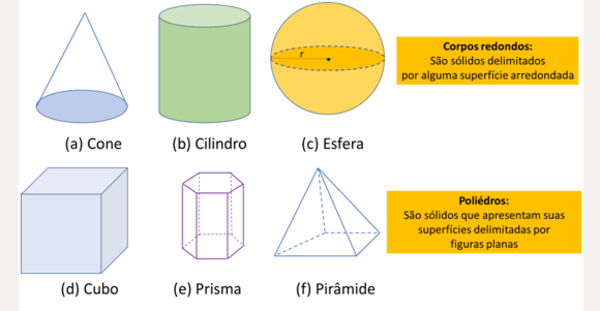
As formas não poliedras ou corpos redondos são aquelas que apresentam em sua superfície, pelo menos, uma parte não plana, isto é, arredondada. Por outro lado, poliedros são figuras geométricas que têm sua superfície formada apenas por partes planas.
Um dos principais objetivos da geometria espacial é determinar, por meio de cálculos matemáticos, o volume e a área desses objetos. Vejamos alguns exemplos, a seguir.
Prismas
No dia a dia, convivemos com vários objetos que são exemplos de forma prismática. São chamados de prismas os poliedros que apresentam bases congruentes e paralelas; essas bases são poligonais.
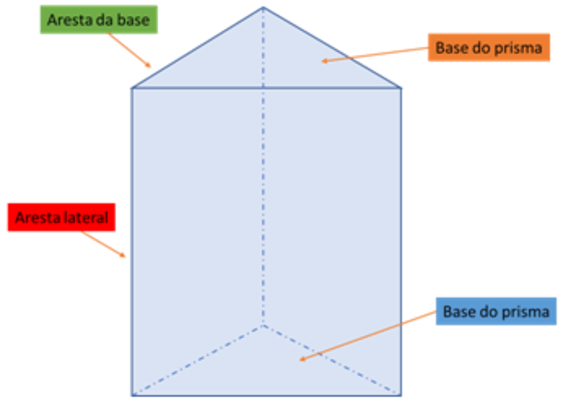
Além dessas características, os prismas também são identificados por apresentarem arestas laterais que ligam as bases. Na figura, abaixo, é apresentado um prisma triangular e seus elementos. Essa classificação ocorre a partir do número de arestas de sua base.
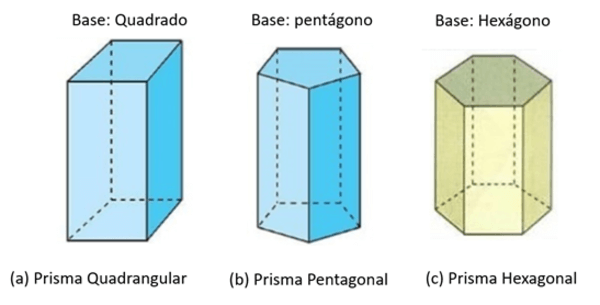
Veja, agora, outros exemplos de prismas com diferentes números de arestas da base.
Prisma reto, oblíquo e seus elementos
A altura de um prisma representa a distância entre os planos que suas bases estão definidas, como mostra a figura.
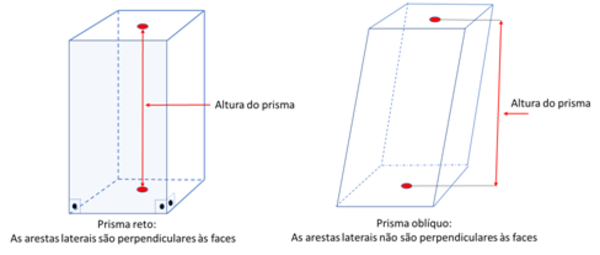
De acordo com a inclinação das arestas laterais, os prismas podem ser retos ou oblíquos. À esquerda, um prisma é identificado como reto quando suas arestas laterais são perpendiculares aos planos que contêm suas bases. Porém, à direita, quando as retas laterais não são perpendiculares aos planos que contêm suas bases o prisma é chamado de oblíquo. O volume do prisma é calculado pelo produto da área da base (Ab) pela altura (h), ou ainda V= Ab . h.
No prisma reto, a atura tem a mesma medida que a aresta lateral.
Paralelepípedo
Paralelepípedos são prismas que têm paralelogramo como base. Para compreender a fórmula do volume do prisma reto, observe a dedução da fórmula do volume de um paralelepípedo retângulo:
V= a . b . c. Mas, a área da base é dada por Ab = a . b. Considerando que a altura do prisma reto é h = c, então, V = 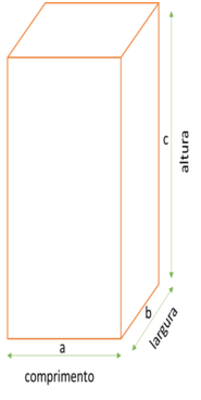 Ab.h.
Ab.h.
Exemplo:
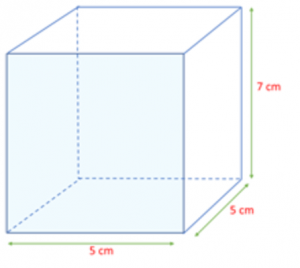
Um prisma quadrangular regular tem 7cm de aresta lateral e 5cm de aresta da base, como mostra a figura, a seguir:
Calculo:
- Área da base
A base do prisma é um quadrado de lado 5cm. Desse modo, a área da base é dada por: Ab = a2 – Ab = 52 – Ab = 25cm2.
- Área lateral
A planificação da superfície lateral é um retângulo de lados 7cm e 20cm. Assim, a área de superfície lateral é dada por: Al = 7.20 – Ab = 140cm2.
- Área total
A área total é dada por: AT = 2.Ab + AL – AT = 2 . 25 + 140 – AT = 190cm2.
- Volume
O volume é dado por: V = Ab . h – V= 25 . 7 – V = 145cm3.
Cubo
Uma forma geométrica conhecida desde a antiguidade, e amplamente usada pelo ser humano, é o cubo. O cubo é um prisma regular, limitado por 6 quadrados congruentes. Como mostra a figura, é um paralelepípedo, cujas dimensões são iguais, ou seja, a = b = c.
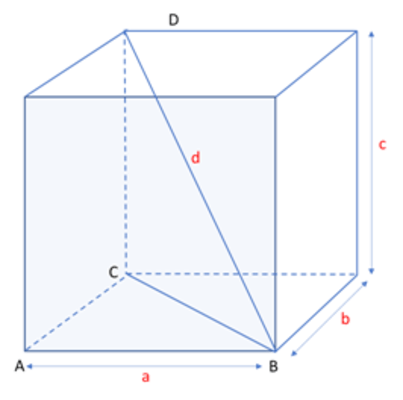
A área total de um cubo de aresta a é dada pela área dos 6 quadrados de aresta a. Ou seja: ATotal= 6 . Aface – 6 . a2
O volume de um cubo de resta a é dado pelo produto da altura (aresta) pela área da base (face), ou seja, V = Ab . h – V= a2 . a – V = a3.
Como o cubo é um prisma retangular, a diagonal de um cubo de aresta a é:
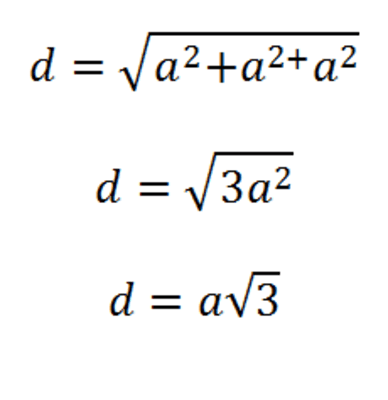
Exemplo:
Se a aresta de um cubo mede 3cm, então:
- A área total é dada por: ATotal = 6 . a2 – ATotal = 6 . 32 – ATotal = 6 . 9 = 54cm2
- O volume é dado por: V = a3 – V = 33 – V = 27cm3
- A diagonal mede:
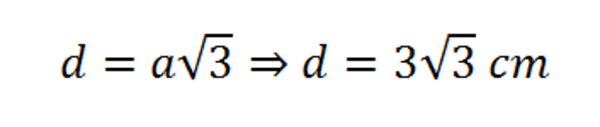
Pirâmide
Uma pirâmide é um sólido delimitado por faces planas, cujas faces laterais são triângulos e a base é um polígono. Elas também podem ser classificadas de acordo com o número de lados dos polígonos da base (pirâmide triangular, quadrangular, pentagonal e hexagonal). A área da superfície total da pirâmide é calculada pela soma da área da superfície da base com a área da superfície lateral: At = Ab + Al
O Volume de uma pirâmide corresponde a um terço do produto da área da base pela altura. Isto é:
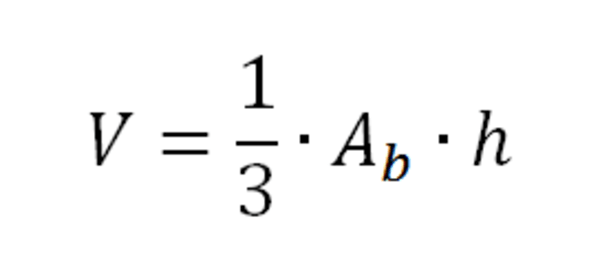
Exemplo:
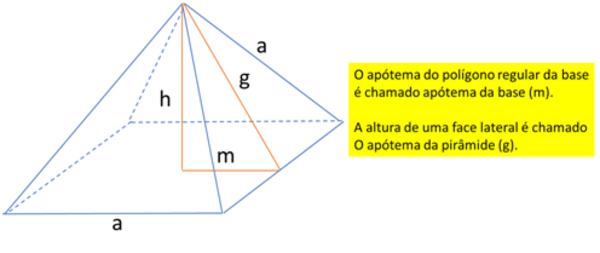
Numa pirâmide quadrangular regular (quando sua base é um polígono regular), a aresta da base mede a =6cm. Sabendo-se que a altura da pirâmide é h = 4cm, calcule a área lateral, a área total e o volume da pirâmide. Veja a figura, abaixo.
Solução
A base da pirâmide é um quadrado. A partir disso, é possível determinar o valor de m tal que,
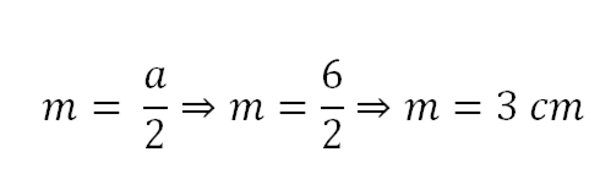
Usando o Teorema de Pitágoras, o apótema da pirâmide (g) é dado por: g2 = h2 + m2, ou seja, g2 = 42 + 32 – g2 = 25 – g = 5cm.
A área lateral de uma das faces é:
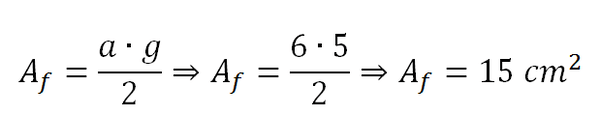
Portanto, a área lateral total é: Al = 4 . Af – Al = 4 . 15 – Al = 60cm2.
Área total é dada por: At = Al + Ab – At = 60 + 36 – At = 96cm2.
Finalmente, o volume é dado por:
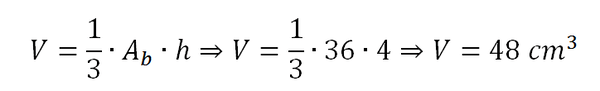








Deixe seu comentário