A sequência de Fibonacci costuma ser trabalhada em aulas de matemática, artes e computação, mas, você sabe o que ela é? A seguir, explicamos detalhadamente seu significado e apresentamos demais informações relevantes a respeito do assunto, aqui no Gestão Educacional!

O que é a sequência de Fibonacci

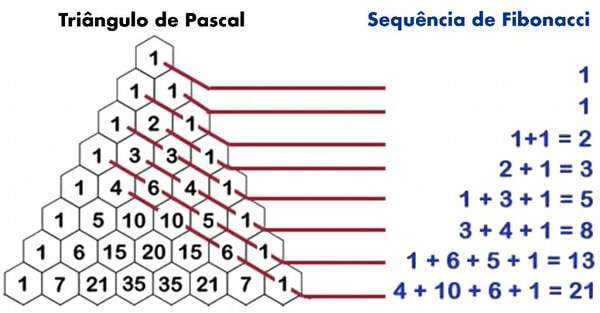
Trata-se de uma sequência de números na qual 1 é o primeiro e o segundo termo, e os demais são resultados da soma de seus dois antecessores. Na prática, a ordem é:

1, 1, 2, 3, 5, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181…

A sequência, que também é chamada de sucessão de Fibonacci, foi transformada em fórmula, para facilitar a identificação de resultados. A representação matemática é Fn = Fn-1 + Fn-2, sendo que F1 e F2 são iguais a 1.

Tal estudo foi criada por Leonardo de Pisa, popularmente conhecido por Fibonacci, no ano de 1202, quando fez uma pesquisa para descrever o crescimento de uma população de coelhos com base em um casal.

Nesse estudo, Fibonacci notou que o crescimento da população se dava exatamente como a sequência, com o resultado da soma dos dois números anteriores.

O grande diferencial da sequência é que ela não se aplica somente nesse caso, mas também a outros fenômenos da natureza, funcionando como uma constante universal de crescimento.

Sequência Fibonacci e o número de ouro

Quando criou a sequência, Fibonacci dividiu um número pelo anterior e constatou que todos os resultados convertem para 1,618, que é considerado um número de ouro, representando não só o crescimento da população de coelhos, mas da evolução da natureza.

Curiosamente, o número de ouro, que também é chamado de Phi, fascina matemáticos e intelectuais há muitos séculos, especialmente quando se fala em crescimento e proporção, conferindo um resultado mais harmonioso.

Prova disso é que o número de ouro foi largamente utilizado na arte, especialmente em pinturas renascentistas, quando se buscava o ideal de perfeição, como em Mona Lisa (Leonardo da Vinci) e O Nascimento de Vênus (Botticelli). Até mesmo Salvador Dalí, em sua obra O Sacramento da Última Ceia, utiliza o número de ouro.

Esse número não se restringe somente à sequência de Fibonacci e à arte: ele está no comportamento de átomos, nas espirais da natureza e na galáxia, nas ondas do oceano, no crescimento de plantas, nas conchas do mar, nas partes do corpo humano, entre outros.

Aplicações da sequência de Fibonacci

São diversos os exemplos de aplicações da sequência de Fibonacci, desde a natureza até o mercado financeiro. Confira, abaixo, onde mais essa ordem numérica é aplicada:

1. Girassol

O miolo do girassol é preenchido com sementes num duplo espiral. Normalmente, encontram-se 21 sementes no sentido horário e 34 no anti-horário, como na sequência de Fibonacci.

2. Concha do caramujo

Cada parte nova da concha do caramujo se caracteriza por ter extensão igual à soma dos dois antecessores, crescendo em proporção harmônica e igual à apontada pela sucessão de Fibonacci.

3. Corpo humano

A divisão da altura de uma pessoa, considerando-se o tamanho médio e não exato, pela distância entre sua cabeça e seu umbigo, terá resultado aproximado de 1,618, que é a divisão de um número pelo seu anterior da sequência Fibonacci.

4. Mercado financeiro

Utiliza-se a sequência Fibonacci e o número de ouro, especificamente seu inverso, para análise de padrões de reversão de ações no mercado financeiro, podendo prever comportamentos e evitar perda de dinheiro.

5. Programação em TI

A sequência Fibonacci também é utilizada em programação de TI, especialmente na linguagem C, C# e C++, que é aplicada no desenvolvimento de jogos 2D, por exemplo.

Outra contribuição de Fibonacci

Durante sua vida, Fibonacci viajou para Grécia, Síria e Egito, especialmente quando mais novo, quando seu pai viajava a negócios. Em uma dessas ocasiões, teve um professor muçulmano que lhe passou conhecimentos matemáticos dos hindus e árabes.

Sua obra Liber Abaci, que apresentou a sequência de Fibonacci, também foi um dos primeiros livros do ocidente a descrever a numeração árabe, introduzindo-a na Europa em substituição a então numeração romana vigente.

No livro, Fibonacci também esclarece o funcionamento de cada numeração, inclusive do zero. Essa introdução dos numerais arábicos é outra contribuição do matemático, uma vez que teve extrema importância para as ciências exatas como conhecemos hoje.