Integrais – O que são? Primitiva, Definidas, Técnicas e Exemplos

Muitos conceitos importantes e problemas da física e engenharia dependem do cálculo da área abaixo da curva de uma função. Por exemplo, a área abaixo da curva de um gráfico da força X deslocamento é justamente o trabalho feito pelo objeto.

Os gregos da antiguidade possuíam grande interesse no cálculo de áreas. Arquimedes utilizava o método da exaustão para calcular a área de uma figura. Mais tarde, Newton e Leibniz trabalharam no que conhecemos hoje como calculo diferencial, e os problemas de Arquimedes encontraram solução mais fácil. As integrais são usadas para resolver problemas como esses. Conheça mais sobre elas, a seguir.

Primitiva de uma função

Seja f uma função definida num intervalo I, uma primitiva de f em I é uma função F, tal que: F’(x) = f(x) – para todo x em I.

Por outro lado, duas funções podem ter derivadas iguais em um intervalo, sendo a diferença entre elas uma constante. Diremos, então, que a família das primitivas de f em I e dada pela seguinte notação: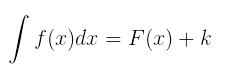Sendo f(x) o integrando e k a constante de integração.

Uma primitiva é também chamada integral indefinida de f. Para encontrar primitivas, podemos utilizar o seguinte artifício: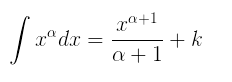Existem algumas propriedades que facilitam os nossos cálculos. Desde que f e g possuam primitivas e seja c uma constante, podemos dizer que: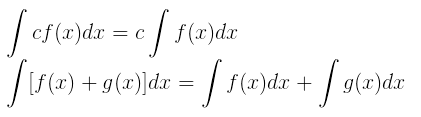

Integrais definidas

Para calcularmos a área abaixo da curva de uma função, utilizamos integrais definidas. A integral definida de f em um intervalo [a,b] pode ser calculada utilizando o 1° Teorema Fundamental do Cálculo:

• Se f for integrável em [a,b] e se F for uma primitiva de f em [a,b], então:

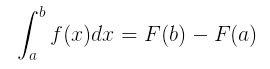Perceba que, nesse caso, não precisamos somar a constante k ao nosso resultado. Porém, em integrais indefinidas é necessário.

Disso, é válido as seguintes propriedades:

• Sejam f, g integráveis em [a,b] e k uma constante, então:

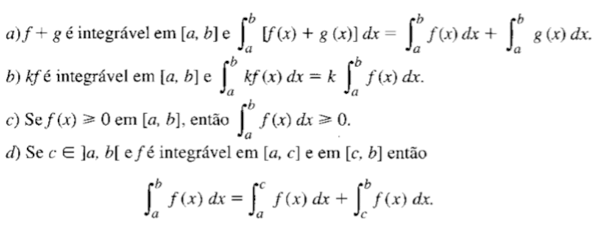
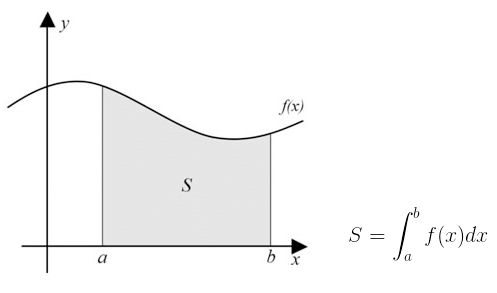
• Seja f continua em [a,b] com f(x) ≥ 0 em [a,b], a área da região S é definida por:

Nem sempre será de imediato obter as primitivas de algumas integrais. Por exemplo, é difícil imaginar qual seria a integral de ∫sen² x + 2cos x . sen 3x dx. Para casos assim, utilizamos as seguintes técnicas de integração:

Mudança de variável na integral definida

Podemos realizar uma mudança de variável para facilitar os cálculos. Seja f contínua num intervalo I e sejam a e b dois reais quaisquer em I, seja g: [c, d] -> I, com g’ continua em [c, d], temos: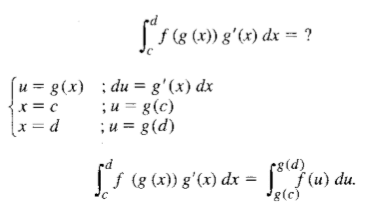

Para entender melhor, podemos analisar um exemplo. Vamos calcular: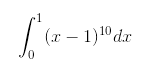Nesse caso, é inviável realizar cálculos para encontrar (x – 1)¹⁰, pois existem métodos mais simples, como a substituição.

Façamos:

x – 1 = u, então x = u + 1

x = u + 1

dx = (u + 1)’ = du

Se x = 0, então 0 =  u + 1 → u = -1

Se x = 1, então 1 = u + 1 → u = 0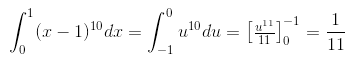

Técnicas de primitivação

Em alguns casos, não é necessário realizar cálculos extensos para a resolução de certas integrais. Uma vez demonstradas, podemos utilizar as primitivas imediatas para encontrar primitivas de modo mais rápido: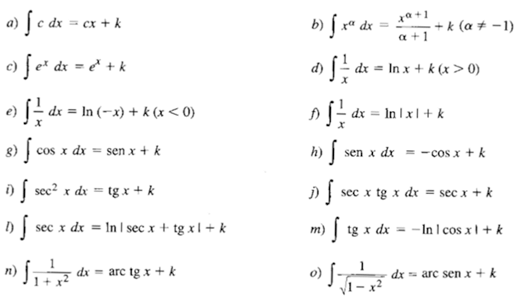Além disso, podemos conferir nosso resultado para verificar se a primitiva obtida está correta. Em uma integral definida, existe apenas uma maneira da sua primitiva ser igual a zero, que é quando a função é limitada por um intervalo do tipo [-r, r]: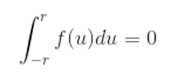Caso os limites de integração sejam, por exemplo, 2 e 4, sua primitiva não será 0.

Além disso, uma integral definida só irá resultar em um valor negativo caso f(x) < 0.

Integração por partes

Suponhamos f e g definidas e deriváveis num mesmo intervalo I. Temos:

[f(x) g(x)]’ = f’(x) g(x) + f(x) g’(x)

Ou

f(x) g’(x) = [f(x) g(x)]’ – f’(x) g(x)

Integrando f(x) g’(x), iremos obter a regra da integração por partes, que é: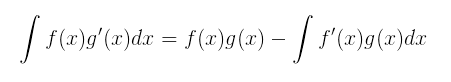Fazendo u = f(x) e v = g(x), teremos du = f’(x) dx e dv = g’(x), o que nos permite escrever essa regra na forma usual: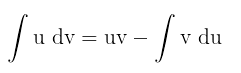

Outras técnicas de integração

Em integrais que envolvem razões trigonométricas, podemos utilizar as identidades trigonométricas, por exemplo:

• Cos 2x = cos² x – sen² x
• Cos² x + sen² x = 1
• Cos² x = ½ + (cos 2x)/2
• Sen² x = ½ – (sen 2x)/2

Podemos utilizar identidades trigonométricas para encontrar primitivas de integrais do tipo ∫(sen 3x)(sen 2x) dx:

cos(a – b) = cos a · cos b + sen a · sen b      (1)

cos(a + b) = cos a · cos b – sen a · sen b      (2)

Fazendo (1) + (2), temos:

Cos a · cos b = 1/2 [cos (a-b) + cos (a+b)]

Fazendo (2) – (1):

sen a · sen b = 1/2 [cos (a-b) – cos (a+b)]

Ainda trabalhando com identidade trigonométricas, podemos calcular integrais do tipo ∫(sen3x)(cos2x) dx.

sen (a + b) = sen (a) . cos(b) + cos (a) . sen (b)      (3)

sen (a – b) = sen (a) . cos(b) – cos (a) . sen (b)        (4)

Fazendo (3) + (4), temos:

sen a · cos b =1/2 [sen (a+b) + sen (a-b)]

Fazendo (3) – (4), temos:

sen b · cos a =1/2 [sen (a+b) – sen (a-b)]