Plano inclinado – O que é? Com e sem atrito, Fórmulas e Exercícios Resolvidos!

O plano inclinado é uma superfície plana, elevada e inclinada. A partir desse plano, é possível estudar o movimento, a aceleração e as forças atuantes em um objeto sob um plano inclinado, que pode ser, por exemplo, uma rampa.

As forças atuantes nesse plano são: a força peso e a força normal, presentes no plano inclinado sem atrito, e a força de atrito, que é levada em consideração ao plano inclinado com atrito.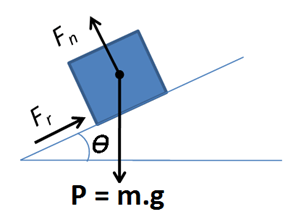

O que é um plano inclinado sem atrito?

O plano inclinado sem atrito apresenta duas forças: uma força vertical para cima, denominada como força normal (N), e uma força vertical para baixo, denominada força peso (P).

Temos, nessa situação, a seguinte fórmula para o cálculo da aceleração: a = g . sen θ, em que:

• a= aceleração;
• g= aceleração da gravidade;
• sen θ = seno do ângulo θ.

Para entendermos tal construção e facilitar o desenvolvimento do cálculo, é necessário colocar o plano inclinado em um o plano cartesiano, com eixos x e y, no qual o peso será decomposto da seguinte maneira:

• Px = P . sen θ (perpendicular ao plano);
• Py = P . cos θ (paralelo ao plano).

Depois disso, é necessário utilizar a Segundo Lei de Newton para calcular a relação entre a força aplicada sobre um corpo e a sua aceleração. Assim, temos, no eixo X: F = m . a (força = massa x aceleração), que pode ser colocada da seguinte maneira: P= m . g (peso = massa x aceleração da gravidade).

Utilizando a fórmula da Segunda Lei com o peso no plano inclinado sem atrito, temos: Px = P . sen θ com  F = m .a.

Assim: P . sen θ = m . a  → em que P também é m . g, assim: m . g . sen θ = m . a.

A partir daí, chegamos à expressão a = g . sen θ.

No eixo Y, temos essa mesma relação, porém com o con θ, uma vez que Py = P . cos θ: Py = m . g . con θ, em que Py pode ser N (força normal), uma vez que, como o bloco não se desloca para baixo e nem para cima, a resultante F = N -P é nula, assim N = P → N = m . g . con θ.

O que é um plano inclinado com atrito?

O plano inclinado com atrito também apresenta duas forças: uma força vertical para cima, denominada como força normal (N), e uma força vertical para baixo, denominada força peso (P). Além dessas duas, há a presença da força atrito, que é calculada a partir da seguinte expressão: Fat=µ.N, em que:

• Fat: força de atrito;
• µ: coeficiente de atrito;
• N: força normal.

Para calcular a aceleração de um objeto num plano inclinado com atrito, utilizamos a seguinte fórmula: a = g . (sen θ – µ . cos θ).

Exercícios Resolvidos

1- Um plano inclinado liso e sem atritos apresenta ângulo de 30º em relação ao solo. Sendo a gravidade local de 10 m/s², determine a aceleração adquirida por um corpo posto a deslizar a partir do topo desse plano.

a) 20 m/s²

b) 5 m/s²

c) 3 m/s²

d) 12 m/s²

e) 2 m/s² 

Resolução: como explicitado na seção teórica deste artigo, a aceleração adquirida por um corpo posto a deslizar sobre um plano inclinado é obtida a partir da gravidade local e do seno do ângulo de inclinação desse plano a = g . sen θ. Sendo a gravidade local de 10 m/s² e o sen 30º = 0,5, temos:

 a = g . sen θ

a = 10 . 0,5

a = 5 m/s²

Resposta: b.

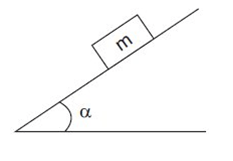
2- (PUC-RIO 2009) Um bloco de massa m é colocado sobre um plano inclinado, cujo coeficiente de atrito estático = 1, como mostra a figura. Qual é o maior valor possível para o ângulo θ de inclinação do plano de modo que o bloco permaneça em repouso?

a) 30º

b) 45º

c) 60º

d) 75º

e) 90º

Resolução: para que o bloco permaneça em repouso, a resultante das forças deve ser 0 (Fr=0). Considerando as forças atuantes para que isso ocorra, temos que:

Px – Fat = 0

Px = Fat

P . sen θ = µ.N

Como N = Py = P . cos θ, substituímos isso na equação:

P . sen θ = µ . P . cos θ

sen θ / cos θ = µ

Pela trigonometria, sabemos que sen θ / cos θ = tg θ. Como dado no exercício, µ = 1, assim, tg θ = 1. Logo, sabendo também que tg 45º = 1, temos que o maior valor possível para o ângulo θ de inclinação do plano, de modo que o bloco permaneça em repouso, é 45º. 

Resposta: b.