Potência – O que é? Relação entre velocidade, Rendimento e Exercícios resolvidos
A potência é a relação do trabalho com o tempo gasto para realizá-lo. Na definição de trabalho, não consideramos o tempo que ele demora para ser realizado, ou seja, o trabalho é o mesmo se realizado em 1 segundo ou 1 ano.
A potência se baseia em uma ideia muito simples: quanto menor o tempo para realizar o mesmo trabalho, maior a potência desenvolvida; quanto maior o tempo, menor a potência.
Por exemplo, uma pessoa que corre 100 metros em 20 minutos pode realizar o mesmo trabalho que um atleta que corre 100 metros em 10 segundos. Basta que cada um exerça sobre seu corpo, em média, a mesma força, pois o deslocamento é o mesmo. O que diferencia o atleta da pessoa sem treinamento é a potência.
O que é potência em física?
A potência foi definida como a razão entre o trabalho e o intervalo de tempo em que ele se realiza. Assim, se uma força F realiza um trabalho τf no intervalo de tempo Δt, a potência média (Pm) dessa força é dada por: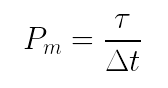 No sistema internacional, o trabalho é dado em joules e o tempo em segundos, a unidade da potência é então o J/s, denominada watt (W), em homenagem ao James Watt.
No sistema internacional, o trabalho é dado em joules e o tempo em segundos, a unidade da potência é então o J/s, denominada watt (W), em homenagem ao James Watt.
Portanto, uma força desenvolve uma potência de 1 Watt quando realiza o trabalho de 1 Joule em 1 segundo.
Como essa unidade é pequena, usa-se com frequência o quilowatt (kW), sendo 1 kW = 1000w.
Relação entre potência e velocidade
O trabalho é a energia transferida pela aplicação de uma força ao longo de um deslocamento. Ele pode ser dado pela seguinte fórmula: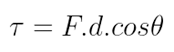 Sendo θ o ângulo que a força faz com o deslocamento.
Sendo θ o ângulo que a força faz com o deslocamento.
Sendo a potência dada por: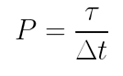 Podemos escreve-la da seguinte forma:
Podemos escreve-la da seguinte forma: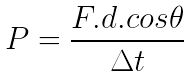 Porém, se o movimento for retilíneo e uniforme, e a força atuar na direção e no sentido do deslocamento, podemos considerar que τ = F. d. Então, a potência pode ser dada por:
Porém, se o movimento for retilíneo e uniforme, e a força atuar na direção e no sentido do deslocamento, podemos considerar que τ = F. d. Então, a potência pode ser dada por: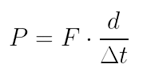 Sendo d = Δx, essa expressão se transforma em:
Sendo d = Δx, essa expressão se transforma em: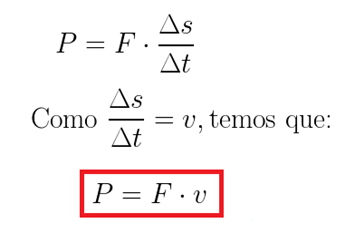 Sendo P a potência (em watt), F a força (em newtons) e v a velocidade (em m/s).
Sendo P a potência (em watt), F a força (em newtons) e v a velocidade (em m/s).
Rendimento
Chamamos de potência útil (Pu) toda a potência fornecida, seja por um motor de automóvel, um organismo, ou qualquer outro exemplo. A potência consumida por esse motor ou organismo para que possam funcionar é chamada de potência total (Pt).
Por definição, a razão entre a potência útil e potência total é chamada de rendimento da máquina, representada pela letra grega η.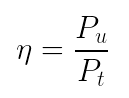 Como a potência útil é sempre menor que a total, o rendimento é sempre menor que 1. Além disso, o rendimento é expresso apenas por um número, sem unidade de medida.
Como a potência útil é sempre menor que a total, o rendimento é sempre menor que 1. Além disso, o rendimento é expresso apenas por um número, sem unidade de medida.
Também, podemos expressar um rendimento em porcentagem: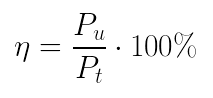 Em geral, o rendimento é a etapa inicial ou final de um problema e exige apenas a percepção do que é consumido ou fornecido pela máquina. Conceitualmente, é importante saber que a máquina ideal, com rendimento igual a 1 (100%), é impossível, o que é objeto de uma lei física estudada na termodinâmica.
Em geral, o rendimento é a etapa inicial ou final de um problema e exige apenas a percepção do que é consumido ou fornecido pela máquina. Conceitualmente, é importante saber que a máquina ideal, com rendimento igual a 1 (100%), é impossível, o que é objeto de uma lei física estudada na termodinâmica.
Exercícios resolvidos
1) A velocidade de um automóvel é constante e igual a 90 km/h. Supondo que a resultante das forças de resistência ao movimento do automóvel seja igual a 3000N, qual a potência desenvolvida pelo motor?
RESPOSTA:
O motor exerce força para vencer a resistência do ar. Por isso, a força R e força F possuem sentidos opostos.
Primeiro, precisamos calcular a força desenvolvida pelo motor para manter a velocidade constante, condição em que a aceleração é nula. Assim, sendo F a força exercida pelo motor e R a resultante das forças de resistência, cujo módulo é R= 3000N, da Segunda Lei de Newton em módulo vem:
F = m . a
F – R = 0
F = R
F = 3000 N
Logo, para v = 90 km/h = 25 m/s, temos:
P = F.v
P = 3000 . 25
P = 75 000 W
2) A potência disponível de uma queda d’água é de 600kW. Qual a potência útil que pode ser obtida dessa queda d’água utilizando uma máquina hidráulica, cujo rendimento é 60%?
RESPOSTA
Em relação à máquina, a potência da queda d’água é a potência total: Pt = 600kW. O que se pede é a potência fornecida pela máquina, ou seja, a potência útil.
Como n%= 60%, temos: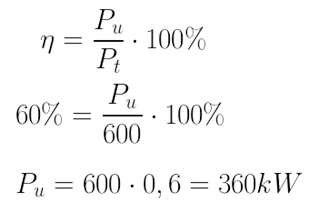









Deixe seu comentário