Potencial elétrico – O que é? Como calcular? Exercícios Resolvidos!
Potencial elétrico é a capacidade que um corpo energizado tem de realizar trabalho, ou seja, atrair ou repelir outras cargas elétricas.
Podemos estudar a ação das cargas elétricas no espaço que as envolve por meio do campo elétrico, que é uma grandeza vetorial. Campos elétricos são regiões onde ocorrem ações ou interações elétricas, provocadas pela ação de cargas. Descrevemos matematicamente um campo elétrico a partir de dois conceitos: o de vetor campo elétrico e o de potencial elétrico.
Em nosso cotidiano, podemos imaginar que o potencial elétrico é algo que não temos contato sempre, porém, a diferença de potencial elétrico é exatamente o que chamamos de voltagem. Em sua casa, com certeza há tomadas de 110V e 220V, que são exemplos de voltagens. A seguir, entenda mais sobre potencial elétrico, só aqui no Gestão Educacional!

O que é energia potencial elétrica?
Quando colocamos uma carga de prova (q) em um campo elétrico, dotamos esse sistema (formado pela carga de prova e pelo campo elétrico) de energia potencial elétrica, ou seja: a força elétrica adquire condições de real trabalho.
Primeiramente, vamos analisar o trabalho realizado sobre uma carga puntiforme num campo elétrico, para depois relacionarmos o trabalho da carga elétrica com a energia potencial elétrica.
Trabalho da força elétrica
Vamos inicialmente obter o trabalho realizado pela força elétrica sobre uma carga de prova (q) em uma trajetória retilínea, ao longo de uma linha d, campo de uma carga puntiforme (Q).
Observe a figura abaixo:
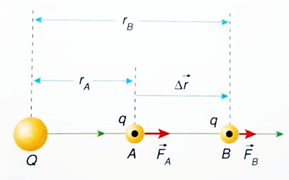
Supomos que as cargas Q e q têm o mesmo sinal. Nessa condição, o trabalho realizado pela força elétrica no deslocamento Δr é motor, pois a força elétrica tem o mesmo sentido que o deslocamento. Uma vez que a intensidade da força elétrica varia com a distância que separamos as cargas, o trabalho é realizado por uma força variável.
Para uma trajetória qualquer entre A e B, como está representado na imagem acima, podemos dizer que:
- O trabalho da força elétrica não depende da trajetória;
- Qualquer que seja a trajetória entre os pontos A e B, o trabalho realizado pela força elétrica é dado por:
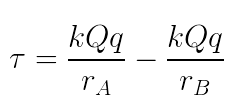 Sendo:
Sendo:
- T: trabalho da força elétrica (J);
- k: constante eletrostática no vácuo (9.109m2/C2);
- Q: carga elétrica fixa (C);
- rA: distância da carga fixa ao ponto A (m);
- rB: distância da carga fixa ao ponto B (m).
Quando a força elétrica é perpendicular à reta tangente da trajetória da carga q, a força elétrica não realiza trabalho sobre a carga de prova. Portanto, temos que: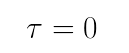 O trabalho da energia potencial elétrica é a diferença entre a energia potencial inicial (no ponto A) e a energia potencial final (no ponto B):
O trabalho da energia potencial elétrica é a diferença entre a energia potencial inicial (no ponto A) e a energia potencial final (no ponto B):
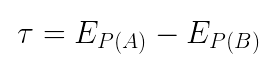
O que é potencial elétrico?
Definimos potencial elétrico (V) de um ponto do espaço como a quantidade de energia potencial elétrica (Ep) por unidade de carga de prova (q) colocada nesse ponto.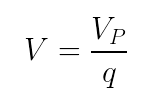 No SI, a unidade de potencial elétrico é o volt (V). O potencial elétrico de 1 volt corresponde à energia de 1 joule por 1 coulomb de carga.
No SI, a unidade de potencial elétrico é o volt (V). O potencial elétrico de 1 volt corresponde à energia de 1 joule por 1 coulomb de carga.
Lembremos que o trabalho da força elétrica é dado por: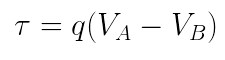 A expressão entre parênteses é denominada diferença de potencial, ou ddp, ou tensão, ou, ainda, voltagem.
A expressão entre parênteses é denominada diferença de potencial, ou ddp, ou tensão, ou, ainda, voltagem.
Comumente, a diferença de potencial VA – VB, é representada por UAB ou, simplesmente, por U: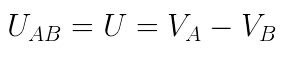 A diferença de potencial (ddp) mede o desnível de potencial elétrico entre dois pontos; é uma grandeza fundamental para o estudo da Eletrodinâmica.
A diferença de potencial (ddp) mede o desnível de potencial elétrico entre dois pontos; é uma grandeza fundamental para o estudo da Eletrodinâmica.
O risco de choques está relacionado com a medida da ddp e não com o potencial elétrico. Se observarmos os pássaros pousados em fios elétricos de alta-tensão não há risco de choque, simplesmente porque, embora o potencial seja alto em relação ao potencial da Terra, nas duas patas de cada pássaro o potencial elétrico é praticamente o mesmo. Não há diferença de potencial, portanto.
Potencial elétrico em campo gerado por partícula pontual
Como vimos acima, para calcular o potencial elétrico, precisamos saber a energia potencial elétrica do sistema de partículas Q e q. Para isso, utilizamos a seguinte fórmula:
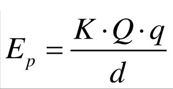
Como V = Ep/q, podemos fazer:
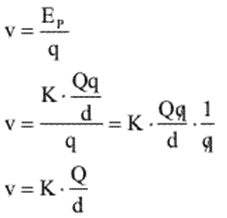
Portanto, podemos definir o potencial elétrico por:
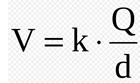
Em que k é a constante eletrostática do meio, cujo valor no vácuo é k = 9.10^9 N.m²/C² e a distância d é medida a partir da posição em que está a partícula de carga Q.
Como o potencial elétrico é uma grandeza escalar, se o campo elétrico for gerado por partículas Q1, Q2 e Q3, o potencial elétrico total em cada ponto desse campo elétrico é obtido pela soma dos potenciais nesse ponto.
Potencial elétrico gerado por uma carga puntiforme
Consideremos uma carga elétrica puntiforme (Q) fixa e um ponto (P) do espaço ao redor dela, seja r a distância entre o ponto P e a carga Q.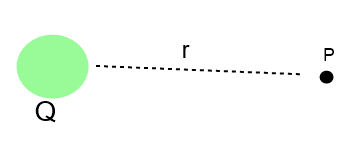 Se colocarmos nesse ponto uma carga elétrica de prova (q), o sistema terá uma energia potencial elétrica dada por: Ep = qVp.
Se colocarmos nesse ponto uma carga elétrica de prova (q), o sistema terá uma energia potencial elétrica dada por: Ep = qVp.
Essa última expressão nos fornece o potencial elétrico de uma carga elétrica puntiforme (Q), em um ponto P, a uma distância r da carga elétrica (q).
Potencial gerado por várias cargas puntiformes
O potencial elétrico de um ponto do espaço sujeito à influência de várias cargas elétricas puntiformes (Q1, Q2, …, Qn), denominadas cargas-fonte, corresponde à superposição do potencial que cada uma delas gele (V1, V2, … , Vn), ou seja:
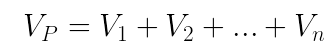
Potencial elétrico em um campo uniforme
Em um campo uniforme, podemos expressar o módulo do vetor campo elétrico da seguinte forma:
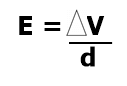
Agora, a unidade de medida do campo elétrico pode ser expressa por volt/metro (V/m).
Potencial elétrico de uma esfera condutora
O potencial elétrico do campo gerado por uma esfera em um ponto externo P é dado por:
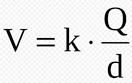
Em que d é a distância do ponto ao centro da esfera.
O potencial no interior do condutor é constante, assim, o potencial de uma esfera condutora em qualquer ponto do interior ou da superfície é o mesmo. Se o condutor tem carga Q e raio r, seu potencial elétrico é:
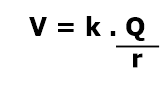
Essas descrições valem para condutores esféricos maciços ou cascas esféricas condutoras.
Diferença de potencial e trabalho em um campo elétrico
A diferença de potencial elétrico entre dois pontos serve para nos informar o que acontece com uma partícula de carga q colocada em um ponto, ou seja, queremos saber se ela vai ou não se mover caso sofra a ação de uma força (F = q.E) causada pelo campo elétrico.
Se o potencial elétrico em um ponto é zero, isso significa que existe uma diferencia de potencial entre esse ponto: à esquerda podemos ter um potencial positivo e à direita um potencial negativo.
Uma partícula q colocada nesse ponto de potencial 0 não vai ficar parada:
- Se q for positiva, tende a se mover para o lado de menores potenciais;
- Se q for negativa, vai para o lado de maior potencial.
A diferença de potencial elétrico entre dois pontos A e B é dada por:
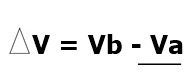
O trabalho mínimo que o agente externo realiza para mover a partícula q é dado por:
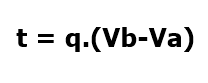
Relação entre trabalho e energia potencial elétrica
O trabalho de uma ou várias forças está relacionado a um determinado deslocamento. Assim, a energia potencial elétrica é:
“O trabalho que pode ser realizado pelas forças elétricas desde a configuração que o sistema tem até uma configuração de referência”.
A configuração de referência é importante para que possamos definir qual é o nível zero de energia potencial. A configuração de referência ocorre quando as cargas estão infinitamente separadas, e quando isso é possível, a energia potencial elétrica é dada por: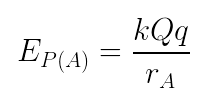
Superfícies equipotenciais
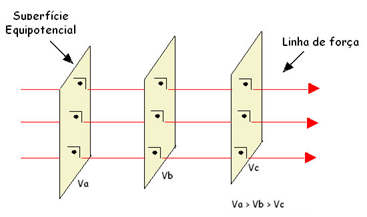
Superfícies equipotenciais são superfícies de um campo elétrico em que todos os seus pontos têm o mesmo potencial.
A visualização de um campo elétrico pode ser feita pelo traçado de linhas de força que contém o vetor campo elétrico tangente a elas. Também podemos utilizar superfícies equipotenciais para visualizar o campo elétrico.
As superfícies equipotenciais são perpendiculares às linhas de força em cada ponto do campo elétrico. Em campos elétricos uniformes, as superfícies equipotenciais são igualmente espaçadas e paralelas entre si. Em campos não uniformes, esse espaçamento é menor nas regiões em que a intensidade do vetor campo elétrico é maior.
Exercícios resolvidos
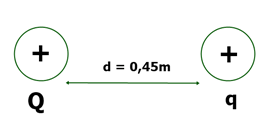
1) Duas partículas pontuais Q e q estão separadas por uma distância d = 0,45m. Elas são cargas pontuais positivas Q = 8.10^-6 C e q = 2.10^-10 C. Determine:
A) a energia potencial elétrica dos sistemas;
B) O potencial elétrico gerado por Q na posição onde está a partícula de carga q.
RESPOSTA:
A) basta aplicar a expressão da energia potencial elétrica:
E = k. (Q.q)/d
E = 9.10^9 . (8.10^-6 . 2.10^-10)/ 0,45
E = 3,2.10^5 V
B) Basta aplicar a expressão do potencial elétrico:
V = k . Q/d
V = 9.10^9 . (8.10^-6/0,45)
V = 1,6 . 10^5 V
2) Uma esfera condutora de raio r = 0,1m está imersa no vácuo. Determine:
A) a capacidade térmica da esfera;
B) a carga armazenada nessa esfera quando ela atinge o potencial de 10 000V.
RESPOSTA:
A) Aplicando a expressão da capacidade térmica da esfera, temos:
C = r/k = 0,1 / 9.10^9
C = 1,1.10^-11 F
B) Da definição de capacidade, temos:
C = Q/V
Q = C.V
Q = 1,1.10^-11 . 1.10^4
Q = 1,1.10^-7 C








Deixe seu comentário