Figuras tridimensionais – O que são? Poliedros, Relação de Euler, Exercícios

A geometria é aplicada em diversas áreas. Um dos exemplos do uso dela em nosso cotidiano é encontrado na arquitetura: como podemos projetar uma casa, um monumento ou um prédio sem o conhecimento das noções geométricas?

Veremos, a seguir, o que são e quais são as figuras tridimensionais e como elas são estudadas na geometria espacial.

Dimensões do espaço – espaço tridimensional

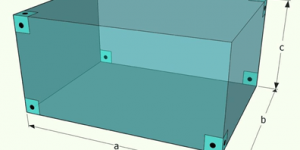
Analise o seguinte exemplo: ao entrar em um cômodo, você pode reparar na quina de duas paredes, como mostra a parte em preto da imagem:

O espaço que vivemos possui três dimensões, ou seja, tem altura, profundidade e largura. A quina dessa parede apresenta exatamente como essas três dimensões se mostram na nossa realidade.

Como o mundo à nossa volta é todo formado por objetos de três dimensões, podemos representar esse espaço tridimensional da seguinte maneira, exatamente como vemos a quina da parede: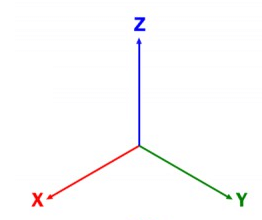

Geometria espacial

No ensino fundamental, geralmente estudamos figuras como quadrados, retângulos, triângulos, círculos etc. Essas formas geométricas fazem parte do estudo da geometria plana, pois são figuras que possuem apenas largura e altura, duas dimensões.

Depois disso, estudamos finalmente a geometria espacial, que trata dos sólidos geométricos que possuem profundidade, além de largura e altura.

Dentre os sólidos geométricos, destaca-se o grupo dos poliedros e o dos corpos redondos. Iremos estuda-los a seguir.

Poliedros: prismas e pirâmides

As figuras abaixo são exemplos de poliedros.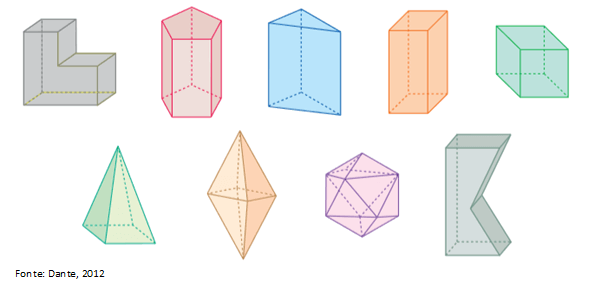Cada poliedro é formado por faces, sendo o número de faces sempre maior ou igual a 4. O encontro desses lados é chamado de vértice.

A linha de encontro entre duas faces é chamada de aresta. Cada vértice do poliedro é um ponto comum a três ou mais arestas.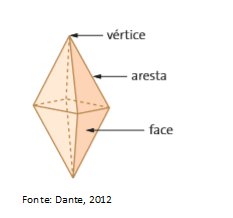Podemos, então, afirmar que poliedros são sólidos de superfícies (faces) planas.

Dizemos que um poliedro não é convexo quando, ao traçar um seguimento ligando dois de seus pontos, o seguimento está sempre contido nele.

Os poliedros convexos são aqueles em que qualquer reta não paralela às suas faces intersecta suas faces em, no máximo, dois pontos.

Veja, a seguir, os exemplos: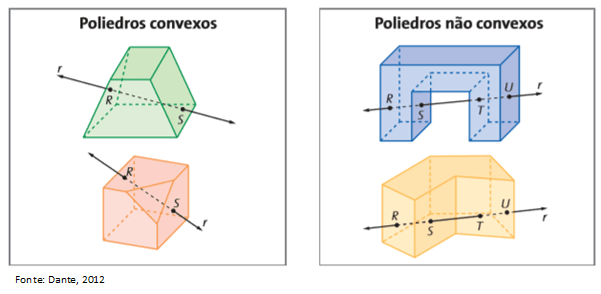

Relação de Euler

Leonahard Euler descobriu uma interessante relação entre o número de faces, arestas e vértices de poliedros convexos: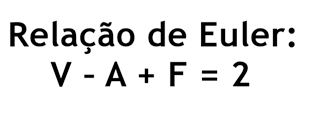Todo poliedro convexo satisfaz a relação de Euler, mas nem todo poliedro que satisfaz essa relação é convexo. Veja, abaixo, um exemplo de poliedro não convexo que satisfaz: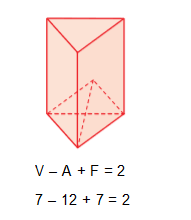

Poliedros regulares

Um poliedro convexo é regular quando todas as faces são polígonos regulares. Além disso, todos os vértices são ligados ao mesmo número de arestas.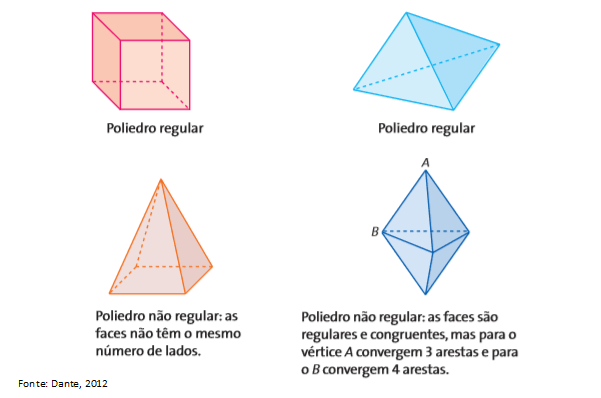Chamamos de poliedro de Platão todos os poliedros em que:

• Todas as faces têm o mesmo número de arestas;
• Todos os vértices ocorrem o mesmo número de arestas;
• Vale a relação de Euler.

Um exemplo de poliedro de Platão é o cubo.

Porém, nem todos as faces precisam ser polígonos regulares para um poliedro ser classificado dessa maneira.

Prismas

Dizemos que um poliedro é um prisma quando ele possui duas faces paralelas e congruentes, ou seja, duas bases iguais. Além disso, suas faces devem sempre ser paralelogramos (lembre-se: retângulos e quadrados são paralelogramos).

Dizemos que um prisma é reto quando as arestas laterais são perpendiculares às bases. Dizemos que é oblíquo quando não são.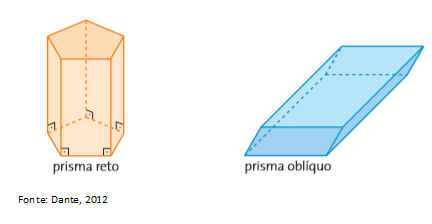Nomearemos os prismas de acordo com as suas bases. Ou seja, se um prisma tem como base uma região quadrada, chamamos ele de prisma quadrangular.

Pirâmides

Pirâmides são poliedros em que suas faces laterais serão sempre triângulos, sendo que elas têm um vértice em comum (a ponta da pirâmide).

Dizemos que uma pirâmide é regular quando sua base é um polígono regular.

Se todas as arestas laterais são congruentes, a pirâmide é reta, caso contrário, ela é oblíqua.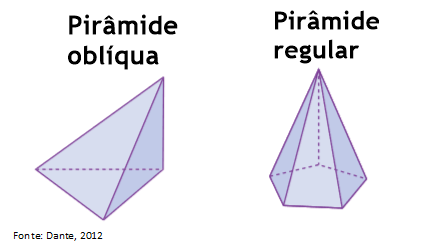

Corpos redondos: cilindro, esfera e cone.

Nem todos os objetos do espaço tridimensional são poliedros. Existem objetos que são limitados por uma superfície arredondada. Esse é o caso dos cilindros, esferas e cones.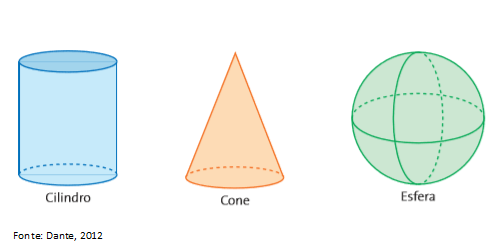O cilindro é formado por duas partes planas, que são suas bases, e uma parte não plana, que é sua lateral “arredondada”.

A reta que passa pelo centro das bases é chamada de eixo. Se o eixo é perpendicular às bases, o cilindro é reto.

O coneé formado por uma parte plana, a região circular que é a sua base, e uma parte não plana, que é uma superfície arredondada (sua lateral).

O eixo do cone é o seguimento que liga o vértice ao centro da base. Se o eixo é perpendicular à base, temos um cone reto. Caso contrário, o cone será oblíquo.

Por fim, temos as esferas, que são delimitadas apenas por superfícies arredondadas.

Exercícios Resolvidos

1) Determine o número de arestas e o número de vértices de um poliedro convexo com 6 faces quadrangulares e 4 faces triangulares.

RESPOSTA:

Como o poliedro tem 6 faces quadrangulares, calculamos:

6 . 4 = 24 arestas.

O poliedro tem 4 faces triangulares:

4 . 3 = 12 arestas.

Como cada aresta foi contada duas vezes, o número total de arestas é:

A = (24 + 12)/ 2 = 18.

Temos, então, F = 10 e A = 18.

Aplicando a relação de Euler:

V – A +  = 2 ⇒ V – 18 + 10 = 2 ⇒ V = 10

Logo, o poliedro tem 18 arestas e 10 vértices.