Força elástica – O que é? Lei de Hooke, Trabalho realizado e Exercícios Resolvidos

Força elástica F_el é a força exercida por um corpo que se deforma, como é o caso da mola. Como a força elástica tende a restaurar o estado relaxado, ela também é chamada de força restauradora.

Na física, classificamos o estudo dos movimentos dos corpos como mecânica, enquanto a cinemática estuda o movimento em si e a dinâmica estuda também as causas desse movimento.

Após Isaac Newton apresentar suas três leis – as Leis de Newton -, a interação entre dois corpos, causada por uma força, passou a ser estudada. Podemos dividir esse estudo das forças nas seguintes categorias:

• Força Peso;
• Força de atrito;
• Força Centrípeta;
• Força Elástica.

E é justamente desta última que trataremos neste artigo do Gestão Educacional: a força elástica.

Muitas forças na natureza possuem a mesma forma matemática que a força de uma mola, portanto, esse estudo nos permite compreender diversos outros fenômenos. Confira!

 O que é força elástica?

Para entendermos tudo o que virá a seguir, observe o seguinte esquema:

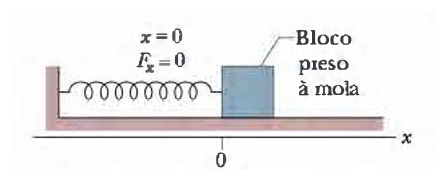
Imagine um suporte onde iremos prender nele uma mola, de modo que essa extremidade presa fique fixa. Teremos também preso na outra extremidade da mola um bloco, que no caso será o representante de um objeto que se comporta como uma partícula.

A mola deve estar no estado relaxado, ou seja, ela não está nem comprimida nem alongada, como mostra a imagem acima.

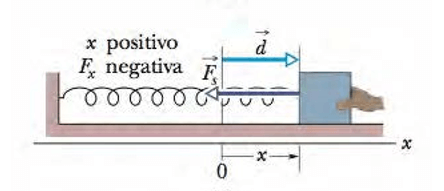
Agora, vamos puxar o bloco para a direita, como mostra a imagem abaixo, de maneira que ele desloque uma medida d.

Ao puxarmos o bloco para a direita, a mola puxa o bloco para a esquerda, pois a força elástica tende a restaurar o estado relaxado.

Se comprimirmos a mola empurrando o bloco à esquerda, a mola irá empurrar o bloco para a direita pelo mesmo motivo apresentado acima.

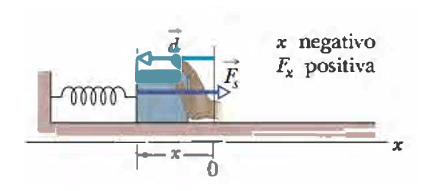
Chamamos essa força restauradora de força F.

Lei de Hooke

Essa interação entre os corpos foi estudada por Robert Hooke, cientista inglês do final do século XVII. Com uma boa aproximação para todas as molas, a força elástica é proporcional ao deslocamento percorrido pela mola desde quando ela estava em estado relaxado até o fim do “puxão” ou “empurrão”.

A força elástica, portanto, é dada por: F = – k . d. Essa fórmula ficou conhecida como Lei De Hooke, sendo Fs a força elástica, k a constante elástica e d a distância percorrida.

O sinal negativo da equação indica que o sentido da força elástica é sempre oposto ao sentido do deslocamento da mola, como podemos observar nas figuras.

A constante k é chamada de constante elástica ou constante de força. Ela é uma medida de rigidez da mola, portanto, quanto maior o valor de k mais rígida a mola é. Isso quer dizer que a força exercida pela mola contra o deslocamento é maior com o aumento do valor de k.

No Sistema Internacional, a unidade de medida da constante elástica é o N/m.

Por fim, d representa a distância entre a posição de relaxamento da mola e a posição final dela após o deslocamento.

Outro modo de escrevermos a a lei elaborada por Robert Hooke é chamar de x a distância percorrida pelo bloco, pois colocamos um eixo x paralelo à mola: Fx = -k.x.

Ao analisar a equação acima, podemos perceber que existe uma relação linear entre a distância e a força elástica. Por exemplo, quanto maior a compressão da mola, maior será a força de restauração oposta à compressão.

Trabalho realizado por uma força elástica

Para determinar o trabalho realizado por uma mola quando o bloco se move, vamos dar a esse objeto um impulso para a direita. A força elástica realiza trabalho sobre ele, diminuindo a energia cinética e desacelerando o bloco.

Porém, como a força elástica é uma força variável, o trabalho não pode ser calculado pela fórmula que conhecemos (W = F.d).

Para determinar esse trabalho, usamos a seguinte equação: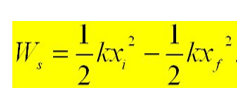

Sendo xi a posição inicial da mola e xf a posição final da mola após o deslocamento. Caso xi = 0 e chamando a posição final de x, podemos escrever também: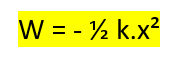

Esse trabalho realizado pode ser positivo ou negativo, dependendo do fato de a transferência total de energia ser do bloco para a mola ou da mola para o bloco.

O trabalho W poderá assumir três diferentes valores:

• O trabalho W é positivo se x_f está mais próxima de x₀ que x_i;
• O trabalho W é negativo se a x_f está mais afastada de x₀ que a posição x_i;
• O trabalho W é nulo se o ponto x_f está na mesma distância de x₀ que x_i está de x₀.

Trabalho realizado por uma força aplicada

Se um bloco está preso a uma mola que se encontra em repouso antes e depois de um deslocamento, o trabalho realizado sobre o bloco pela força responsável pelo deslocamento é dado por: W_a = – W_s

Sendo W_a o trabalho realizado pela força sobre o bloco e W_s o trabalho realizado pela força elástica.

Exercícios Resolvidos

1) O trabalho realizado para mover uma mola de sua posição inicial Xi=0 para a posição final Xf = 4m é de 15 N. Determine a constante elástica dessa mola.

R: W = – ½ k.x²

15 = – ½ k. (4)²

15 = – ½ k. 16

15 = -16/2 . K

15 = -8.k

K = -15/8 N/m

2) Um bloco preso a uma mola de massa desprezível percorreu uma distância de 28 centímetros, alongando a mola. Sabendo que a constante elástica da mola é igual a 300 N/m, determine o valor da força elástica. Interprete esse resultado.

Como estamos alongando a mola, teremos a distância d positiva e igual a 0,28m.

Fx = -k.x

Fx = -300.0,28

Fx = -84 N

A força está negativa porque o sentido dela está no sentido negativo ao eixo x, ou seja, ela é contrária à força que puxou o bloco.